Una búsqueda por Internet con las claves “monte carlo simulación” nos proporciona cerca de 200 mil resultados (búsqueda efectuada con google, junio de 2017). En la mayoría de los casos los correspondientes artículos se centran en las virtudes matemáticas. Aunque es cierto que las raíces de la técnica Monte-Carlo provienen de éstas, nos centramos aquí en los aspectos prácticos.
En primer lugar queremos resumir los casos donde una simulación Monte-Carlo puede resultar ser muy útil.
• Estimar la gama de posibles resultados antes de tomar una decisión
• Pronosticar resultados financieros
• Estimar la duración de un proyecto
• Simplemente comprender la variabilidad de un proceso o sistema
• Y de ahí, encontrar problemas en un proceso o sistema con del fin de proporcionar una solución, basándose en datos.
Básicamente la simulación consiste en asignar valores aleatorias a variables dentro de un rango especificado. Antes de entrar en grano con un ejemplo más versátil, mostraremos la esencia básica de antemano.
Imagínese que tengamos una zapatería que vende entre 120 y 190 pares de zapatos cada mes y que por cada par de zapatos vendidos se obtiene un beneficio de 20 Euros. El rango de beneficio oscila
entonces entre 120 x 20 = 2.400 Euros y 190 x 20 = 3.800 Euros. Una simulación recurre ahora a los números aleatorios para asignar a los diferentes números de pares de zapatos los beneficios
correspondientes. Imaginémonos entonces que una simulación con 5 iteraciones nos haya proporcionado los siguientes resultados:
| N. de iteración | Pares de zapatos |
Beneficio por zapato (Euros) |
Beneficio total (Euros) |
| 1 | 121 | 20 | 2.420 |
| 2 | 145 | 20 | 2.900 |
| 3 | 166 | 20 | 3.320 |
| 4 | 172 | 20 | 3.340 |
| 5 | 178 | 20 | 3.560 |
En este simple caso, donde solamente una variable es incierta (pares de zapatos), ya queda expuesto la esencia básica de una simulación. Con técnicas estadísticas seremos capaz de analizar los resultados con más detalle. Así observamos que en ningún caso hemos obtenido un beneficio total mayor a 3.700 Euros (vendiendo el equivalente a 180 pares de zapatos). Analógicamente podremos constatar que el 50% del beneficio total es menor a 3.320 Euros (correspondiente a las iteraciones 1 y 2) o equivalente, que el 50% del beneficio total es mayor a 3.320 Euros (correspondiente a las iteraciones 4 y 5).
Lo cierto es que con solamente 5 iteraciones nuestros resultados son poco fiables. Pero el método de las simulaciones no nos impide a hacer cientos o miles de iteraciones, con lo cual los resultados serán cada vez más de fiar. El quid de una simulación es identificar qué variables con inciertas y cómo se comportan.
Hemos de reconocer que la herramienta Excel de Microsoft ya proporciona por sí misma casi todas las virtudes para arrancar una simulación dentro del mismo entorno. Con MC FLO en cambio
proporcionamos una herramienta que hace de las simulaciones una tarea fácil.
Ahora entramos en grano. Supongamos que una tienda virtual venda un artículo por internet y que el precio de éste se establece según un algoritmo acorde a la demanda. En la siguiente tabla
mostramos las unidades vendidas y sus correspondientes precios de las primeras cinco semanas del año anterior.
| Unidades | Precio por unidad |
| 1.437 | 189,05 |
| 1.448 | 189,96 |
| 1.358 | 189,29 |
| 1.436 | 189,81 |
| 1.297 | 190,68 |
En el siguiente fichero Excel vemos todos los datos de las últimas 150 semanas. Nuestro objetivo es predecir los ingresos para el próximo año, asumiendo que las futuro nos ampara el idéntico abanico de posibilidades como el del pasado.
En primero lugar vamos a asignar a las unidades vendidas una distribución apropiada con MC FLO. Marcamos los datos y después de un breve instante MC FLO nos proporciona una distribución
triangular como segundo mejor resultado.
La distribución triangular requiere como parámetro el valor mínimo, máximo y el de mayor frecuencia. Como se ve abajo, hay pocas ocurrencias cerca del mínimo. En cuanto vaya creciendo el valor hasta el valor de mayor frecuencia, las ocurrencias van aumentando para después decrecer hasta el umbral máximo. La distribución triangular es quizás la más fácil de comprender e la más intuitiva.
Conviene reproducir la fórmula con el asistente gráfico y – dado que los valores solo representan una muestra – corregir los umbrales. Alternativamente podemos recurrir a la distribución definida por el usuario que refleja los datos de forma empírca en vez de forma analítica.
Los mismo haremos ahora con los precios. Dado que suponemos que éstos se forman independientemente de los precios de las semanas anteriores, procedemos con el método de asignar a la variable una distribución de forma automática, que será del tipo normal. Sin embargo, una simulación tiene poco valor si no somos capaces de reconocer que pueda haber correlaciones entre diferentes variables. Como podemos comprobar fácilmente y recurriendo fórmulas básicas de Excel, hay una correlación lineal negativa entra las variables "unidades" y el "precio por unidad" (se observa entonces que cuando los precios son altos, las unidades vendidas disminuyen y viceversa) y que usaremos introduciendo con MC FLO la correspondiente correlación con el asistente gráfico.
Los ingresos se obtienen finalmente multiplicando las unidades por el precio, ambas variables inciertas y por lo tanto se les asignarán valores aleatorios durante la simulación. No obstante, hemos de matizar aquí dos cosas. Primero: para obtener el ingreso por semana se debe de recurrir a la técnica de la convolución. Esto significa que los precios aleatorios de deben de multiplicar con las unidades aleatorios por cada ocurrencia. Si no la volatilidad se dispararía (imagínese que en la iteración i un total de 1'400 unidades son calculados; a cada unidad hay que asignarle entonces un precio diferente; de lo contrario asumiríamos que todas las 1'400 unidades se venden por el mismo precio, lo cual no es lógico). Segundo: Dado que nuestro objetivo es pronosticar los ingresos para el próximo año, mas las unidades solamente están disponibles semanalmente, hemos de multiplicar el valor incierto por 52 (semanas por año). Eso lo hacemos directamente en la variable de salida (un técnica más elaborada sería incluir la estacionalidad de las ventas).
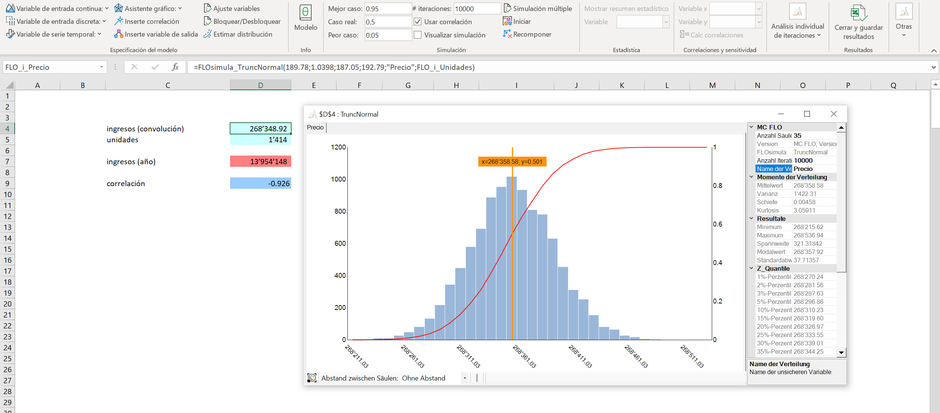
Nuestro modelo está ahora completo. Para mayor transparencia MC FLO ha asignado a todas las variables un nombre y coloreado las celdas correspondientes. Ahora toca arrancar la simulación, que la haremos con 10.000 iteraciones. (Aquí no mostraremos todas las posibilidades de MC FLO, para mayor información pueda consultar el video de enseñanza).
Centrémonos en los ingresos anuales, que al fin de cuentas es el resultado que más interesa. Éstos oscilan entre 11 y 17 millones de Euros con una media de 14 millones (véase los resultados a la derecha del histograma). Adicionalmente observamos que existe una probabilidad del 70%, de que los ingresos sean inferiores a 14 millones, lo cual también se traduce en una probabilidad de 30% que se puedan obtener ingresos mayores a 14 millones de Euros.
Estas afirmaciones no serían posible sin las simulaciones. El contexto clásico de las calculaciones en Excel solo nos permite a asignar a cada variable un valor determinado y no un rango de
posibles valores. Una calculación con simulaciones, sin embargo, posiciona entonces el resultado en un contexto (probabilidad, que algo ocurre es mayor a....). Así mismo se ha de
constatar que con simulaciones somos capaces de entender mejor un problema o - mejor dicho - seremos capaces de revelar resultados que sin la simulación no nos hubiéramos imaginado. Les invitamos
a entrar en el mundo de las simulaciones. Cargue las versión de prueba y vea lo fácil que es.
Nota: Hemos usado MC FLO en castellano, pero con el perfil del idioma alemán puesto. Algunas palabras aparecen por lo tanto en dicho idioma.




Kommentar schreiben