Das Moving-Average Modell – dem Zufall auf der Spur

In einer unserer letzten Blogs haben wir das AR (autoregressive) Zeitreihenmodell vertieft und anhand eines praktischen Beispiels dargelegt, wie die Momentenmethode mit MC FLO umgesetzt ist. An dieser Stelle möchten wir dies für den MA (moving-average) Zeitreihenprozess nachholen.

Ein MA Prozess der ersten Ordnung besteht aus einer wiederkehrenden, gleichbleibenden Grösse - dem Erwartungswert - und einer Zufallskomponente, welcher über den Zeitablauf miteinander korreliert und den Erwartungswert überlagert. Das Besondere bei einem MA Prozess ist, dass nicht die ersichtlichen Grössen (also das Ergebnis) miteinander in Beziehung stehen, sondern die nicht beobachtbaren Zufallswerte. Der MA Prozess unterscheidet sich dabei fundamental vom Namensvetter des «gleitenden Durchschnitts», welches als deterministisches Verfahren gilt und von einer Zufallskomponente bewahrt bleibt.

Hier der Versuch eines Beispiels zum MA(1) Prozess: Stellen Sie sich vor, dass Sie Kaffeekapseln verkaufen und der Absatz im Mittel 200‘000 beträgt. Neben dem direkten Verkauf bieten Sie auch Gutscheinmarken (mit Verfallsdatum) an, welche den Absatz fördern sollen und von Dritten im Umlauf gebracht werden. Jede Gutscheinwerbung kann individuell vom Drittanbieter gestaltet und mit anderen Produkten gekoppelt werden. Sie können somit den Markt für Gutscheine für Ihre Kapseln nicht direkt beobachten. Im Fall eines MA(1) Modells wird der Absatz in der aktuellen Periode von der Anzahl Gutscheinkampagnen in dieser Periode und mit einer Gewichtung auch von der Gutscheinkampagne der letzten Periode einfliessen (sprich, die in der letzten Periode abgesetzten Gutscheine werden in dieser Periode vor Verfall noch eingelöst; bei einem MA(2) Modell würden Sie die letzten zwei Perioden betrachten müssen). Der beobachtbare Gesamtabsatz setzt sich somit aus dem Grundabsatz (hier 200'000) und dem Absatz aus den Gutscheinkampagnen zusammen.

Im folgenden Excel haben wir die Logik von MC FLO in Bezug auf das MA(1) Modell aufbereitet. In Spalte B haben wir 35 normalverteilte Zufallszahlen mit einem Mittelwert von 50‘000 und einer Standardabweichung von 5‘000 abgebildet. Der MA Prozess soll so ausgestaltet sein, dass der Mittelwert der Grundkomponente 200‘000 beträgt und die Zufallszahl der Vorperiode mit einem Gewicht von 0.6 einfliesst. Damit haben wir das oben generisch beschriebene Kaffeebeispiel abgebildet. Spalte C greift diese Zufallszahlen auf und bildet anhand der in Zelle A1 eingegebenen Formel den entsprechenden MA Prozess ab. Für das theta - also dem Gewicht der Vorperiode – wird anhand der Momentenmethode ein Wert von 0.09 und für die Standardabweichung ein Betrag von 7‘623 ausgewiesen. Eine Ermittlung der Parameter über MC FLO liefert die gleichen Zahlen. Gegenüber den echten Parametern von 0.6 und 5‘000 somit doch eine relativ hohe Abweichung. 

Zur Validierung der Momentenmethode können wir das bessere Schätzverfahren

«Maximum Likelihood» heranziehen und einen Vergleich erstellen. Hierfür haben wir das Open Source Tool «gretl» verwendet. Für das theta wird ein Wert von 0.48 und für die Standardabweichung ein solcher von 7‘767 ermittelt. Zumindest in Bezug auf die Gewichtung (theta) ist das Maximum Likelihood der Momentenmethode überlegen. Dass beide Verfahren relativ schlecht die Modellparameter abschätzen, liegt an der geringen Grösse der Testdaten (35 Beobachtungen) und der Spezifikation des Zufallsterms. Im Vergleich zum Maximum Likelihood ist aber nicht die Abweichung der Parameter von primärer Relevanz, sondern die Fähigkeit, auf Basis des gewählten Modells und der Parameter eine geeignete Schätzung vorzunehmen. Für das 95% Konfidenzintervall errechnet gretl für den fünften Prognosetag eine untere Schranke von 264‘424 und eine obere Schranke von 296‘819. Mit 10‘000 Iterationen und die Batch Funktion von MC FLO nutzend, kommen wir auf Werte von 266‘512 und 295‘970 (wenn Sie dies nachrechnen, werden Sie vielleicht auf andere Werte kommen, was natürlich der Simulation geschuldet ist). Das sind durchaus vergleichbare Aussagen und doch auf den ersten Blick erstaunlich, denn bei einem theta von 0.48 wird augenscheinlich die Vorperiode stärker gewichtet als bei einem Wert von 0.09. Dies sollte doch zu einer viel höheren Abweichung führen, oder?

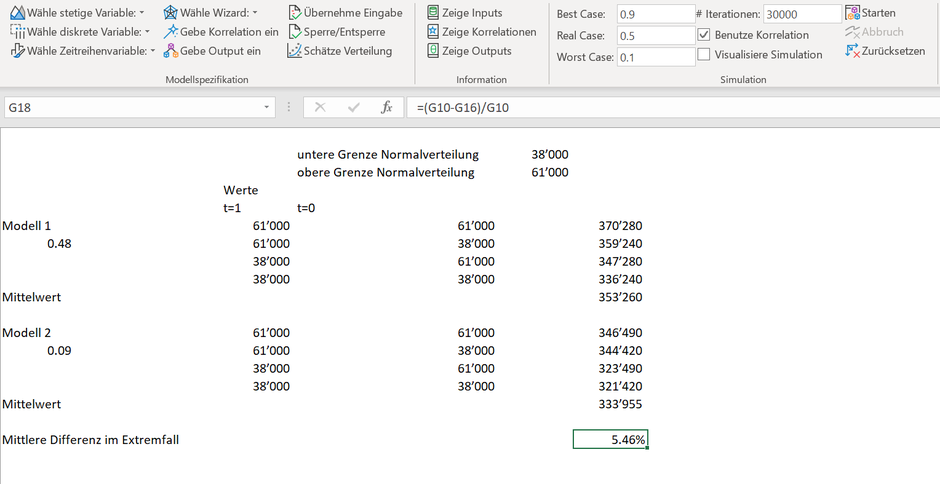
Wenn wir die normalverteilte Zufallsvariable (Mittelwert von 50‘000 und Standardabweichung von 5‘000) in der Praxis auf das 98% Perzentil beschränken, erhalten wir 38‘000 als untere und 61‘000 als obere Grenze. Nachstehend haben wir die vier möglichen Extremkonstellationen und die Auswirkungen auf einen MA(1) Prozess mit einem Theta von 0.48 und 0.09 dargestellt. Die mittlere Differenz beträgt beim Heranziehen des Minimum und des Maximum gerade mal 5.46%, wobei auf einen errechneten Erwartungswert von gerundet 280‘000 in beiden Modellen abgestützt wird (die Details können den Formeln des Excels entnommen werden). Es liegt auf der Hand, dass nicht nur allein das theta als Mass für ein gutes Modell herangezogen werden sollte. Aus dieser praktischen Überlegung sind wir überzeugt, dass die Momentenmethode auch für das MA(1) Modell ausreichend ist.

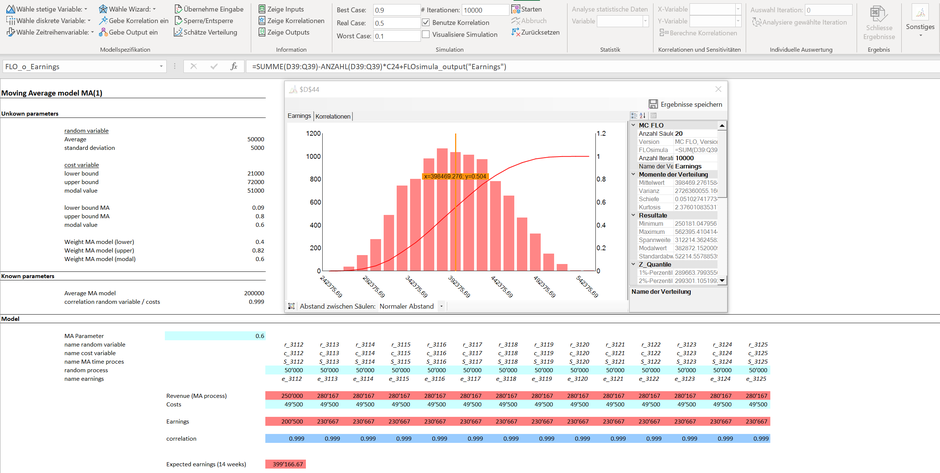
Im Regelfall sind Phänomene wie die Gutscheinkampagnen nicht unabhängig von anderen Grössen, welche beispielweise den Gewinn eines Unternehmens beeinflussen. So wird je Gutscheinkampagne ein Betrag an den ausgestellten Betreiber fällig. Je höher die Anzahl oder Umfang der Gutscheinkampagnen, desto höher die Kosten für das betroffene Unternehmen. Hier ist im Gegensatz zum AR Prozess aber nicht der gesamte Absatz von Kaffeekapseln, sondern nur die durch Gutscheinkampagnen ausgelösten Absätze relevant. Daher sind die Zufallszahlen je Periode mit den entsprechenden Kosten, hier vereinfacht als PERT-Verteilung modelliert, zu korrelieren. Grundsätzlich möchten wir davon ausgehen, dass die Zahlungen an die Veranstalter nur von den Kampagnen abhängig sind. Da eine nahezu perfekte Korrelation besteht und die Ursache auch eindeutig ist, haben wir einen Korrelationskoeffizienten von 0.999 herangezogen^[1]. Somit können wir die Auswirkungen einer Gutscheinkampagne auf unseren Gewinn direkt als Simulation risikobasiert in MC FLO modellieren. Hierbei macht es natürlich Sinn, dass die Gewichtung der Vorperiode als Bestandteil des MA Prozesses ebenfalls variabilisiert wird, da wir bei der Simulation die unsicheren Vorkommnisse (hier die Einlösequote aus der Vorperiode) möglichst umfassend berücksichtigen sollten. Analog oben haben wir auch hier eine PERT Verteilung mit Modalwert von 0.6 angesetzt. Nach Durchlauf von 10‘000 Iterationen über den Vorschaumodus und unter Berücksichtigung der Korrelation kommen wir auf einen zusätzlichen Gewinn von im Mittel 43 TCHF (wir haben jeden Absatz mit 1 CHF angesetzt und andere Grössen, wie etwa eigene Vertriebskosten etc. vernachlässigt). Wichtiger ist hierbei aber die Beobachtung, dass die Kosten für die Gutscheinkampagnen in den meisten untersuchten Fällen geringer als der Mehrertrag ausfallen. Sprich, mit einer 70%-Sicherheit ist eine Gutscheinkampagne für den Kaffeekapselhersteller profitabel. In dieser Konstellation durchaus einleuchtend, da die Korrelation zwischen den Kosten der Kampagnen und Mehrertrag eindeutig positiv und nur auf Kampagnen – nicht jedoch auf die eingelösten Gutscheinmarken - beschränkt sind.

 ^[1] Eine Korrelation von genau +1 oder -1 lässt sich mit einer entsprechenden Funktion direkt in Excel umsetzen und wird in MC FLO als solches auch nicht unterstützt. Zudem ist es häufig so, dass Rechtsstreitigkeiten, Garantiefälle oder andere Phänomene eine perfekte Korrelation in der Praxis ausschliessen.  

P.S. Wir müssen zugeben, dass die Ökonomie von Gutscheinen eine viel kompliziertere als die hier dargestellte Vereinfachung ist. Die kritischen Leser mögen uns dies verzeihen.