El modelo de medias móviles - qué casualidad

En uno de nuestros últimos blogs hemos profundizado el modelo de series temporales AR (autorregresivo), ilustrando un ejemplo práctico de cómo se implementa el método del los momentos en MC FLO. En este apartado lo vamos a hacer para las medias móviles, abreviado MA.

Un proceso del MA(1) de primera orden se compone de un valor, lo podemos llamar valor esperado, y un componente al azar, que se imponen al valor esperado. Lo especial acerca de un proceso de MA(1) es que los componentes al azar están correlacionados entre sí mismos y no los valores observables como ocurre en el modelo AR. 

Veamos un ejemplo del proceso MA(1): Imagínese un vendedor de cápsulas de café y que el promedio de ventas por periodo es de 200.000. Aparte de la venta directa, también ofrece sellos de cupones (con fecha de vencimiento) con la intención de promover las ventas y éstos son distribuidos por terceros. Cada promoción de cupón puede diseñarse individualmente y combinarse con otros productos. Por lo tanto, no puede controlar directamente el mercado de cupones para sus cápsulas. En el caso del modelo MA(1) y relacionado con el mercado de las cápsulas se ha de considerar por lo tanto que la venta está relacionada con el número de campañas de cupones en el período actual, y con una ponderación dependiendo asimismo de la campaña del período anterior.

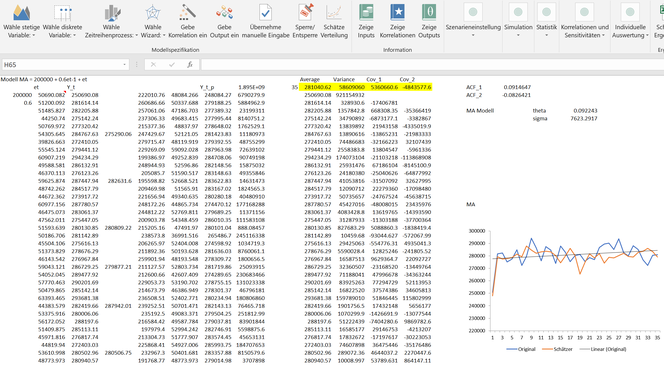
En el siguiente Excel hemos preparado la lógica de MC FLO en relación con el modelo MA(1). En la columna B hemos proyectado 35 números aleatorios normales con una media de 50.000 y una desviación estándar de 5.000. El proceso MA(1) debe diseñarse de manera que el valor medio del componente fundamental sea 200.000 y el número aleatorio del período anterior se incluya con un peso de 0,6. Con esto, hemos reproducido el ejemplo descrito anteriormente. La columna C recoge estos números aleatorios y usa la fórmula ingresada en la celda A1 para trazar el proceso de MA(1) correspondiente. Para el theta, es decir, el peso del período anterior, se muestra un valor de 0,09 usando el método del los momentos y una cantidad de 7.623 para la desviación estándar. La determinación de los parámetros a través de MC FLO proporciona los mismos resultados. Comparado con los parámetros reales de 0,6 y 5.000, observamos entonces una desviación relativamente alta. 

Para validar el método de los momentos podemos usar el método de estimación llamado "máxima verosimilitud". Para esto usamos la herramienta de código abierto "gretl". Para el theta se determina un valor de 0,48 y para la desviación estándar uno de 7.767. Al menos con respecto a la ponderación (theta), el método de la máxima verosimilitud es superior al método de los momentos. El hecho de que ambos métodos estiman relativamente mal los parámetros del modelo se debe al pequeño tamaño de los datos de prueba (35 observaciones) y la especificación del término aleatorio. Sin embargo, en comparación con la máxima verosimilitud, no es simplemente la desviación de los parámetros la que tiene mayor relevancia, sino la capacidad de realizar una estimación adecuada en función del modelo y los parámetros elegidos. Para el intervalo de confianza del 95%, gretl calcula para el quinto día de previsión un límite inferior de 264.424 y un límite superior de 296.819. Con 10.000 iteraciones y usando la función por lotes de MC FLO, llegamos a unos valores de 266.512 y 295.970 correspondientes (si re-calcula esto, puede obtener otros valores, que por supuesto se debe a la simulación). Estas son afirmaciones bastante similares y, sin embargo, a primera vista sorprendentes, porque con un theta de 0,48, el período anterior pesa más que con un valor de 0,09. Esto debería conducir a una desviación mucho mayor, ¿verdad?

Si limitamos la variable aleatoria (media de 50.000 y desviación estándar de 5.000) en la práctica al intervalo de confianza del 98%, obtenemos 38.000 como el límite inferior y 61.000 como el límite superior. A continuación, presentamos las cuatro posibles constelaciones extremas y los efectos en un proceso MA(1) con un theta de 0.48 y 0.09. La diferencia de media es solo del 5,46% usando el mínimo y el máximo, basado en un promedio de 280.000 en ambos modelos (los detalles se pueden encontrar en las fórmulas del Excel). Es obvio que no solo el theta debe usarse como una medida para un buen modelo. Dado el resultado de esta consideración práctica, estamos convencidos de que el método de los momento es suficiente para el modelo MA(1). 

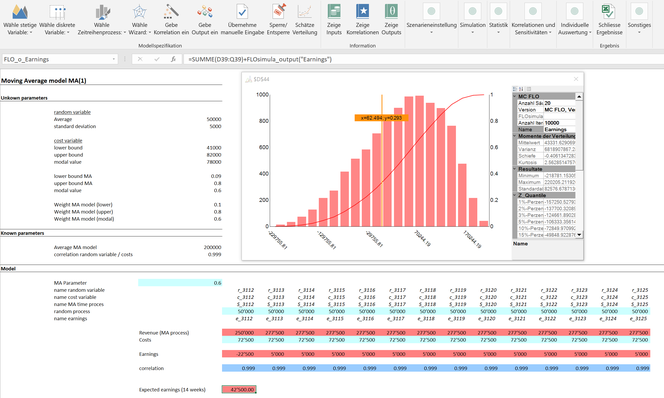
Por regla general, fenómenos como las campañas de cupones no son independientes de otras variables que, por ejemplo, influyen en los beneficios de una empresa. Para cada campaña de cupones se ha de abonar una compensación al emitente. Cuanto mayor sea el número o el tamaño de las campañas de cupones, mayores serán los costes para la empresa en cuestión. Por lo tanto, los números aleatorios por período deben correlacionarse con los costes correspondientes, aquí simplificados con una distribución PERT. Como norma general, asumimos que los pagos a los emitentes solo dependen de las campañas. En consecuencia, solo el fabricante de la cápsula de café se beneficia de los cupones canjeados más tarde. Como hay una correlación casi perfecta y la causa también es clara, se utilizó un coeficiente de correlación de 0,999 ^[1] entre la variable aleatoria y los costes.

Dado que a priori no sabemos cual va a ser el theta empírico, nos conviene simular también la ponderación. Por convención hemos establecido una distribución PERT con un valor modal de 0,6 para el theta. Después de haber ejecutado 10.000 iteraciones a través del modo de la vista previa de MC FLO, y teniendo en cuenta la correlación obtendremos un beneficio adicional de un promedio de 43 mil. Más importante que la ganancia adicional es la observación de que los costes de las campañas de cupones son en la mayoría inferiores a los ingresos adicionales. Tenemos un 70% de certeza, que una campaña de cupones es rentable para el fabricante de cápsulas de café.  

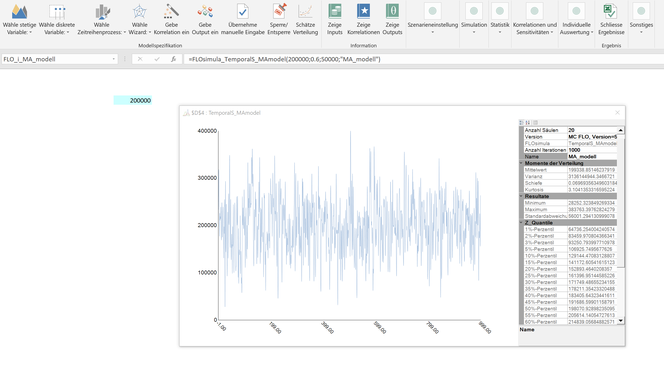
En MC FLO, puede usar el proceso MA(1) como parte integral de una simulación de variable única. En ese caso no necesita definir las variables individualmente. Una simulación integrada es particularmente útil si necesita hacer pronósticos para el futuro habiendo obtenido el proceso y los correspondientes parámetros anteriormente con la función de estimación incorporada en MC FLO. 

^[1]Una correlación de exactamente +1 o -1 puede implementarse directamente en Excel con una función correspondiente, pero no es posible asignar tal correlación en MC FLO. Litigios, casos de garantía u otros fenómenos impiden una correlación perfecta en la práctica.

Nota: Debemos admitir que la economía de los cupones es mucho más complicada que la simplificación presentada aquí.