Zeitreihen - richtig einsetzen

Von einigen Kunden haben wir Rückfragen zu der Handhabung von MC FLO mit Zeitreihen bekommen. Im vorliegenden Beispiel gehen wir anhand eines einfachen Beispiels den typischen Fragestellungen auf den Grund.

Mit MC FLO haben wir ein Produkt erstellt, das kinderleicht zu bedienen ist und es auch in Zukunft bleiben soll. Daher verzichten wir bewusst auf Formeln oder Konstrukte, die im täglichen Gebrauch mit Excel bei vielen Kopfzerbrechen bereitet. Als Paradebeispiel kann die Array-Funktion genannt werden, mit der sich logisch angeordnete Werte in Excel darstellen lassen. Gewichtige Nachteile von Array-Funktionen sind die umständliche Handhabung und die fehlende Transparenz über die Ermittlung der einzelnen Elemente eines Arrays bei einer Simulation. Mit dem Verzicht auf Array-Funktionen in MC FLO müssen daher andere Wege bei der Modellbildung eingeschlagen werden.

Schauen wir hierzu folgendes Beispiel an:

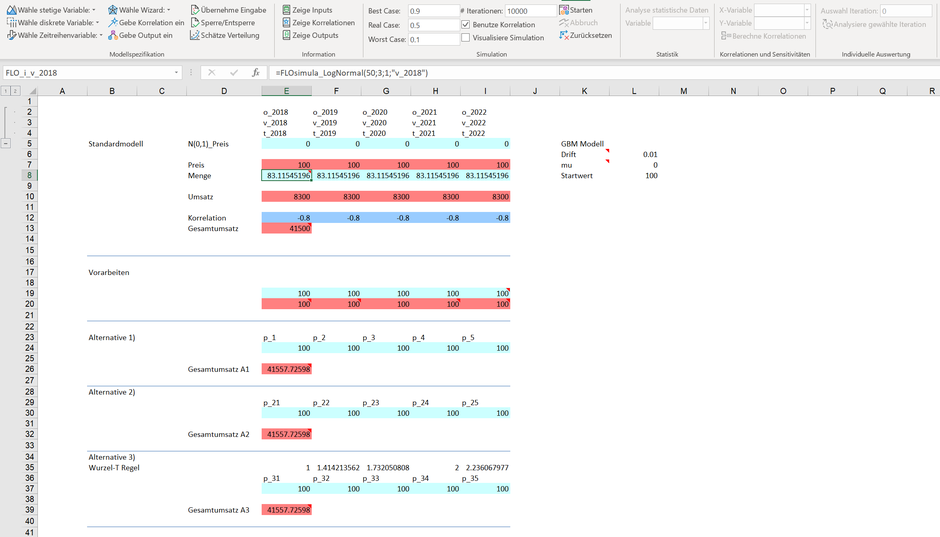
Sie haben als Aufgabe den Umsatz eines Produktes für die nächsten fünf Perioden zu planen. Sowohl der Preis als auch die Menge gelten als unsicher. Für die Menge unterstellen Sie eine Lognormal-Verteilung. Für die Preisbildung wollen Sie eine geometrische brownsche Bewegung mit Startwert 100 annehmen (alle Parameter können dem beigelegten Excel entnommen werden). Excel-Profis würden nun erwarten, dass diese mittels Array Funktion in den Zeilen E7:I7 einzutragen ist. Nicht so bei uns. 

Mit MC FLO haben Sie mehrere Möglichkeiten, die Array-Funktion zu umgehen und trotzdem eine robuste und möglichst korrekte Herleitung der geometrischen brownschen Bewegung mit einfachen Handgriffen in Excel abzubilden.

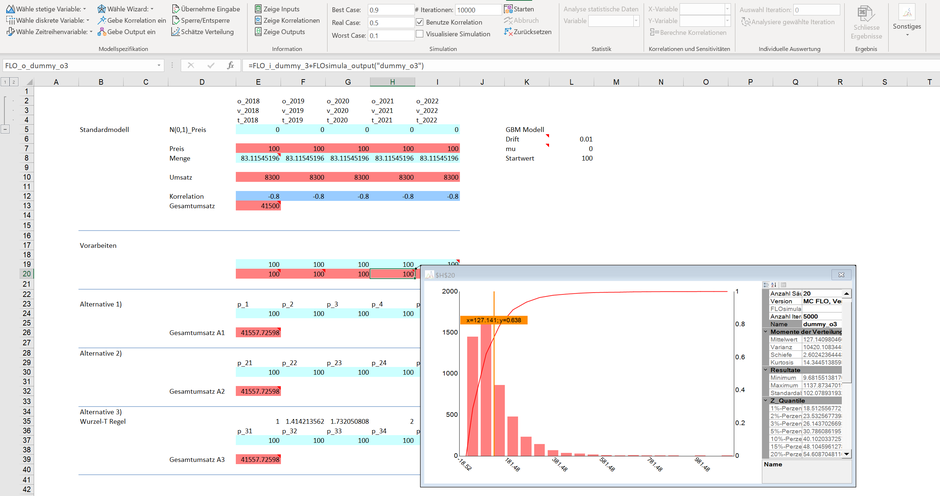
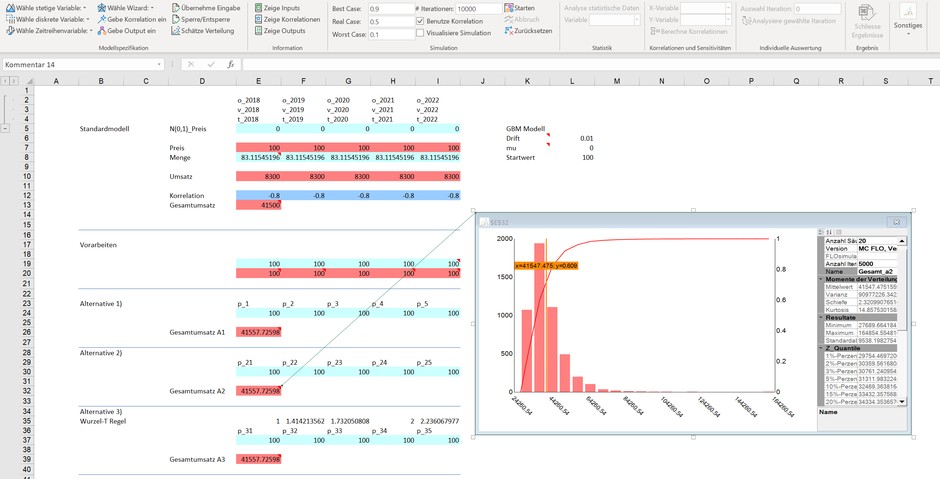
Die erste Strategie besteht darin, dass für jedes Plandatum eine eigene Zeitreihenformel eingeben wird, was wir in den Zeilen E24:I24 vorgenommen haben (Alternative 1). Als Besonderheit haben wir als Startwert die vorangegangene Zelle herangezogen und das Flag beim Parameter „UseBefore“ auf 1 gesetzt. So wird sichergestellt, dass der errechnete Wert des Vorgängers (etwa Zeile E24) als Startwert für die nächste Periode herangezogen wird (Zeile F24). Was auf den ersten Blick einleuchtend klingt, bedarf jedoch einer Klarstellung, denn die in den Zellen E24:I24 eingegebenen Formeln ändern sich bei jeder Iteration. Wenn Sie beispielweise eine Simulation mit 5‘000 Iterationen durchführen möchten, bedeutet dies in unserem Fall, dass die in der Zeile E24 eingetragene Formel einen Wert zwischen ca. 9 und 1’137 Geldeinheiten annehmen kann, was wir folgend mit der Vorschaufunktion in Zelle H20 veranschaulicht haben.

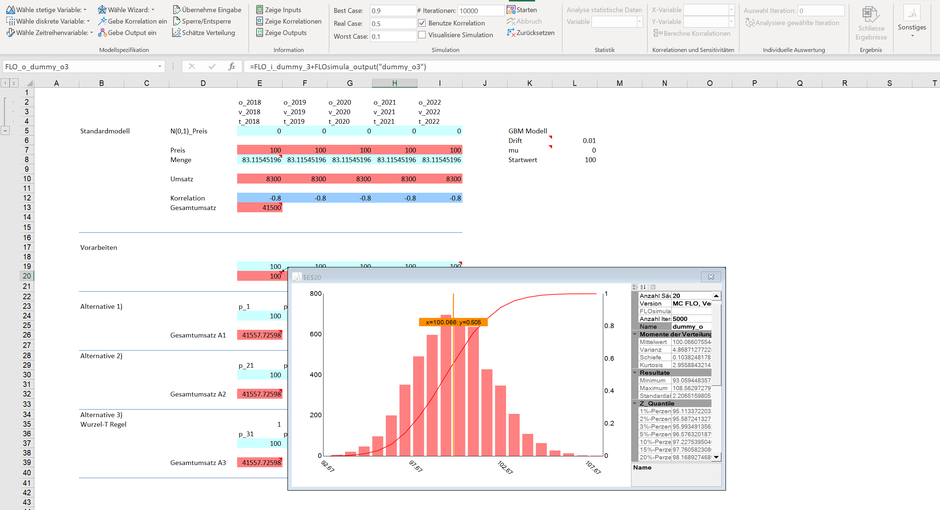
Die Logik ist dabei denkbar einfach: Eine Simulation mit 5‘000 Iterationen einer Zeitreihenvariablen ist gleichbedeutend mit der Ermittlung einer Zeitreihe über 5‘000 Perioden! In fünf aufeinanderfolgenden Perioden ist aber mit der genannten Parameterkonstellation nicht mit einer derartigen grossen Abweichung zu rechnen. Wenn Sie schon explizit mit Zeitreihen in diesem Fall arbeiten möchten, gibt es zwei Auswege: die erste besteht darin, dass Sie die Formel für die einzelnen Variablen anpassen (indem Sie etwa den Drift Parameter massiv kürzen). Somit können Sie einen realistischeren Verlauf der Preisentwicklung über die fünf Perioden auch bei mehreren tausend Iterationen nachbilden. Wie kommen wir dabei auf die neuen Parameter? In Zeile E21 haben wir das Resultat der Zeitreihe mit den Ausgangsparametern der geometrischen brownschen Bewegung über die fünf Perioden nach 5‘000 Iterationen dargestellt. Die Werte schwanken dabei zwischen ca. 93 und 108. 

In Zeile I19 haben wir durch Ausprobieren neue Parameter für eine geometrische brownsche Bewegung eingegeben, welche bei 5‘000 Iterationen ungefähr bei den oben genannten Werten von 93 und 108 zu liegen kommen. Das Resultat kann der Zelle I20 entnommen werden. In den Zellen E24:I24 haben wird diese neue Formel eingetragen. Das Resultat über die an die Anzahl Iterationen angepasste geometrische brownsche Reihe können Sie der Zelle E26 entnehmen, womit die Alternative 1 umfassend beschrieben ist.

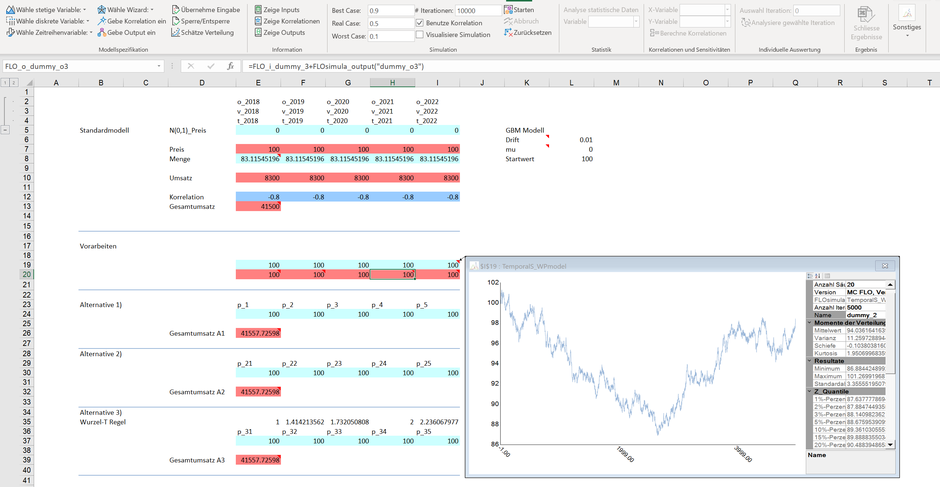
Die zweite Möglichkeit besteht darin, dass Sie in der ursprünglichen Formel die Anzahl der Perioden als zusätzlichen Parameter angeben und den Startwert bei 100 belassen (Alternative 2). Diese Alternative haben wir in den Zeilen E30:I30 nachgestellt. So lautet für die zweite Periode die Formel wie folgt „=FLOsimula_TemporalS_WPmodel(100;0.01;0;1;0;"p_22";2)“, wobei die 2 vor der schliessenden Klammer die Anzahl Perioden definiert. Bei jedem der 5‘000 Iterationsläufen wird hierbei beginnend mit Startwert 100 der Wert für die zweite Periode (per Ende) gerechnet. In Zelle I30 erfolgt die gleiche Logik für die fünfte Periode.

Beide Möglichkeiten über die Zeitreihen haben einen gewichtigen Nachteil: Sie müssen zuerst eine Transformation vornehmen (im ersten Fall) oder sind in der Lage nur beschränkt Korrelationen (im zweiten Fall) zu berücksichtigen. Wir haben noch zwei andere Möglichkeiten....

Die dritte Möglichkeit besteht darin, die möglichen Ausprägungen in jeder Planperiode mittels einer Dichte – respektive Verteilungsfunktion abzubilden. Die geometrische brownsche Bewegung verläuft einer Log-Normalverteilung (die Preise sind niemals kleiner 0), die Renditen (also die Abweichungen zwischen zwei Perioden) hingegen einer Normalverteilung. Wenn wir die Preisentwicklung der fünf Perioden als Ergebnis einer Renditeverteilung interpretieren, können wir für die Preise approximativ eine Normalverteilung heranziehen, wobei die Standardabweichung mit der Zeit anhand der Wurzel-T Regel zunimmt. Diese Alternative ist in den Zeilen E37:I37 abgebildet (Alternative 3). Dabei haben wir uns zur Bestimmung der Parameter der Normalverteilung der gleichen Logik wie in Alternative 1 beholfen. In Zeile G19 haben wir die möglichen Ausprägungen der Zeitreihen über eine Periode dargestellt. Das Resultat kann aus Zelle G20 entnommen werden. Die Werte schwanken zwischen 96 und 104. Der Planumsatz mit dieser Variante ist in Zelle E39 ersichtlich. 

Die letzte und von uns favorisierte Lösung besteht darin, die Preisentwicklung direkt anhand der Formel für die geometrische brownsche Bewegung in Excel abzubilden, was wir in den Zellen E7:I7 mittels Outputvariablen vorgenommen haben. Ausgangspunkt ist eine Standardnormalverteilung, welche beginnend mit Zelle E5 zu der gesuchten Grösse zusammengesetzt wird. Mit dieser Variante haben Sie eine einwandfreie Herleitung garantiert. 

Für alle Alternativen als auch für die Standardlösung haben wir die Formeln einmalig manuell und dann mittels der Funktion «Übernehme manuelle Eingabe» automatisiert in Excel und MC FLO registriert (siehe hierzu auch folgendes Video [auf Englisch]). Damit ist sichergestellt, dass die Eingabe fast so schnell erfolgt wie mit der Eingabe über eine Array-Funktion. Der Vorteil: Sie haben gegenüber der Array-Funktion alle Variablen, auch die Zufallsterme einer Zeitreihe, transparent gemacht und können so viel besser die Zusammenhänge erkennen.

Wir möchten zudem davon ausgehen, dass zwischen Preis und Menge eine hohe negative Korrelation von -0.8 bestehen soll. Da wir die Zufallsterme der Zeitreihe in der präferierten Lösung kenntlich gemacht haben, können wir eine entsprechende Korrelation zwischen der Menge und dem Zufallsterm der geometrischen brownschen Bewegung ohne weiteren Aufwand abbilden. So einfach. Mit MC FLO sind Sie in der Lage zu erkennen, welche Variablen massgeblich den Gesamtumsatz über alle fünf Perioden beeinflussen, was im Tornado Diagramm von MC FLO kenntlich gemacht wird. Sie können somit eine fundierte Entscheidung treffen. So sehen wir, dass wir nur zu 13% sicher sein können, dass der Planumsatz höher als 50'000 Geldeinheiten zu liegen kommen wird und der grösste Einfluss auf den Umsatz die Preisgestaltung ausübt. 

Im Blog zum AR(1), MA(1) und hier zur geometrischen brownschen Bewegung (GBM) haben wir die notwendigen Werkzeuge aufgezeigt, wie Sie mit MC FLO spielerisch Zeitreihen ohne den Rückgriff auf eine Array-Funktion produktiv einsetzen können. Mit den in MC FLO eingebauten Zeitreihen sind Sie zudem in der Lage, für individuelle Variablen mehrere tausend Perioden zu simulieren oder noch wichtiger, Prognosen zu erstellen. Besonders hierfür sind die Zeitreihen in MC FLO gedacht.

P.S: Wenn Sie die Korrelation zwischen der Menge in 2018 («v_2018») und dem Preis für 2018 («p_2018») näher betrachten, werden Sie feststellen, dass die Korrelation nicht -0.8 beträgt, was zu einem darauf zurückzuführen ist, dass der Preis nur zu Teilen aus der Zufallskomponente zusammengesetzt ist, zum anderen aber auch an den Verteilung der beiden Variablen, welche eine exakte Korrelation gemäss Spezifikation erschwert. Wir empfehlen zudem, dass Sie das Referenzmodell ohne die Alternativen separat speichern und dann eine Simulation starten. So haben Sie nur die Variablen in der Arbeitsmappe berücksichtigt, welche für das Modell relevant sind. Der Transparenz wird es behilflich sein.