De algunos clientes nos han llegado incógnitas sobre el manejo de MC FLO con series temporales. En el presente blog llegaremos a la raíz de las preguntas típicas acompañados por un simple ejemplo.
De antemano queremos mencionar que con MC FLO hemos creado un producto que es muy fácil de usar y que debería seguir siéndolo en el futuro. Por lo tanto, evitamos conscientemente fórmulas o construcciones que causan muchos dolores de cabeza en el uso diario con Excel. Como tal, llama la atención la función de matrices, con la cual es posible agrupar valores en cadena. Considerables desventajas de las función de matrices son el manejo complejo y la falta de transparencia sobre la determinación de los elementos individuales de una matriz. Evitando las función de matrices en MC FLO requiere por supuesto formas alternativas al determinar un modelo que incorpore la incertidumbre de manera adecuada.
Echemos un vistazo al siguiente ejemplo:
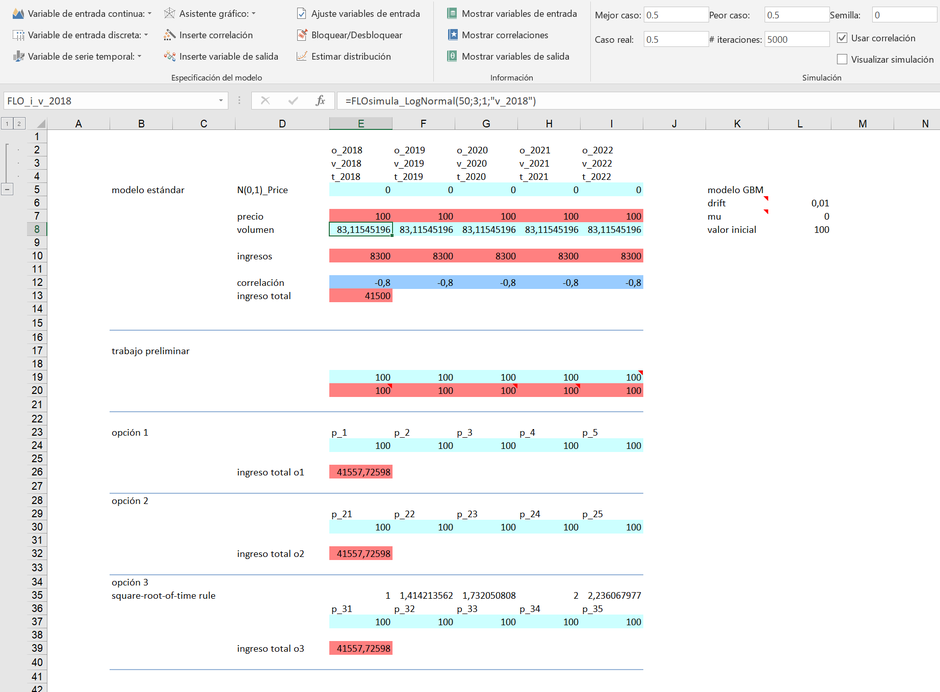
Usted tiene la tarea de planificar las ventas de un producto para los próximos cinco períodos. Tanto el precio como la cantidad se consideran inciertas. Para el volumen asuma una distribución lognormal, en cuanto a la evolución del precio se inclina hacia un movimiento browniano geométrico con un valor inicial de 100 (todos los parámetros se pueden tomar del Excel adjunto). Los profesionales de Excel esperarán que la evolución de los precios se resuelva usando la función de matrices en las columnas E7: I7. No es así en nuestro caso.
Con MC FLO tiene varias opciones para eludir la función de matrices y aún así asegurarse de una derivación sólida de un movimiento browniano geométrico siguiendo unos simples pasos en Excel.
La primera estrategia es introducir la fórmula de la serie temporal llamada movimiento browniano geométrico para cada período por separado, lo cual hicimos en las columnas E24: I24 (opción 1). Como característica especial hemos utilizado la celda anterior como valor inicial del siguiente periodo, indicándolo con el parámetro 1 en "Use before". Esto asegura que el valor calculado del predecesor (por ejemplo en la celda E24) se utiliza como el valor de inicio para el próximo período (celda F24). Lo que parece obvio a primera vista, sin embargo, requiere una aclaración. Los valores de las fórmulas introducidas en las celdas E24: I24 cambian en cada iteración. Si desea realizar una simulación con 5.000 iteraciones, por ejemplo, significa que en nuestro caso el valor de la fórmula introducida en E24 puede tener un rango entre aproximadamente 5 y 1.415 unidades de precio. Dicho resultado se puede rastrear en el comentario introducido en la celda H20.
La lógica de este comportamiento es muy simple: una simulación con 5.000 iteraciones es equivalente a la determinación de una serie temporal sobre 5.000 períodos. Sin embargo, en cinco períodos consecutivos - que es lo que nos interesa - no se puede esperar una desviación tan grande con la constelación de parámetros según el modelo inicial. Si se desea trabajar con la serie temporal directamente y de forma explícita, hay dos maneras de resolver este enigma: la primera consiste en ajustar la fórmula correspondiente (acortando como tal el parámetro que regula la desviación). Así podrá modelar un progreso más realista del desarrollo de los precios durante los cinco períodos, incluso con varios miles de iteraciones. ¿Cómo hemos obtenido los nuevos parámetros? En la celda E20 hemos guardado el resultado del movimiento browniano geométrico durante los cinco períodos después de 5.000 iteraciones. Los valores varían entre aproximadamente 93 y 108.
En la celda I19 hemos introducido nuevos parámetros siguiendo la estrategia “trial and error” que tiene como resultado un rango de precios entre aproximadamente 93 y 108 al curso de 5.000 iteraciones. El resultado de la distribución se puede tomar de la celda I20. En las celdas E24: I24 la nueva fórmula ha sido introducido de forma correspondiente. El resultado de los ingresos sobre los cinco períodos usando la fórmula para el movimiento browniano geométrico se puede encontrar en la celda E26.
La segunda opción consiste en identificar el número de períodos en la fórmula original como un parámetro adicional y dejar el valor inicial en 100 (opción 2). Hemos trazado esta alternativa en las columnas E30: I30. Para el segundo período, la fórmula se muestra como "=FLOsimula_TemporalS_WPmodel (100; 0,01; 0; 1; 0;" p_22 "; 2)", donde el 2 antes de la paréntesis de cierre define el número de períodos. Para cada una de las 5.000 iteraciones, el valor para el segundo período se calcula a partir del valor inicial. En la celda I30 la misma lógica se sigue para el quinto período.
Ambas opciones usando la fórmula directa del movimiento browniano geométrico tienen ciertos inconvenientes: en primer lugar, debemos realizar una transformación (en el primer caso) o la posibilidad de implementar correlaciones queda reducida.
Tenemos otras dos posibilidades...
La tercera opción consiste es mapear las características de cada período por medio de una función de densidad o distribución. La serie temporal “movimiento browniano geométrico” sigue una distribución log-normal (los precios nunca son menores que 0), mientras que la rentabilidad (es decir, la diferencia de precios entre dos períodos) sigue una distribución normal. Si interpretamos la evolución de los precios durante los cinco períodos como el resultado de una distribución de retorno, podemos utilizar una distribución normal con la condición de que la desviación estándar aumenta con el tiempo siguiendo la regla raíz de T. Esta alternativa se muestra en las columnas E37: I37. Al hacerlo, usamos la misma lógica implementada en la opción 1 para determinar los parámetros de la distribución normal. En la celda G19 hemos trazado la fórmula con posibles parámetros cuyos resultados se reflejan en la celda G20. Los valores fluctúan entre 96 y 103. El ingreso correspondiente se puede ver en la celda E39.
La última y mejor opción consiste en trazar el desarrollo del movimiento browniano geométrico usando la fórmula directamente en Excel, lo cual hicimos en las celdas E7: I7. El punto de partida es una distribución normal estándar que, comenzando con la celda E5, se ensambla al conjunto deseado.
Para todas las alternativas, así como para la solución estándar, hemos insertados las fórmulas de forma manual y luego registrándolas en Excel y MC FLO de forma automática usando la función
"Ajuste variables de entrada" (véase también el siguiente video en
inglés). Esto garantiza que el modelo sea construido de forma tan rápido como usando la función de matrices. La ventaja en nuestro caso: todas las variables, incluidos los términos aleatorios de
una serie temporal quedan transparentes, lo cual facilita la comprensión del modelo.
¿Y correlaciones?
Queremos finalmente asumir una correlación negativa de -0.8 entre el precio y el volumen. Tal como hemos identificado en la solución preferida los términos aleatorios de la serie temporal por separado, ahora estamos dispuestos a mapear una correlación correspondiente entre el conjunto y el término aleatorio del movimiento browniano geométrico sin más esfuerzo. Así de fácil. Con MC FLO podrá observar a continuación qué variables influyen en las ventas totales durante los cinco períodos. Por lo tanto, podrá tomar una decisión más informada.









Kommentar schreiben