Von Risiken und Portfolios

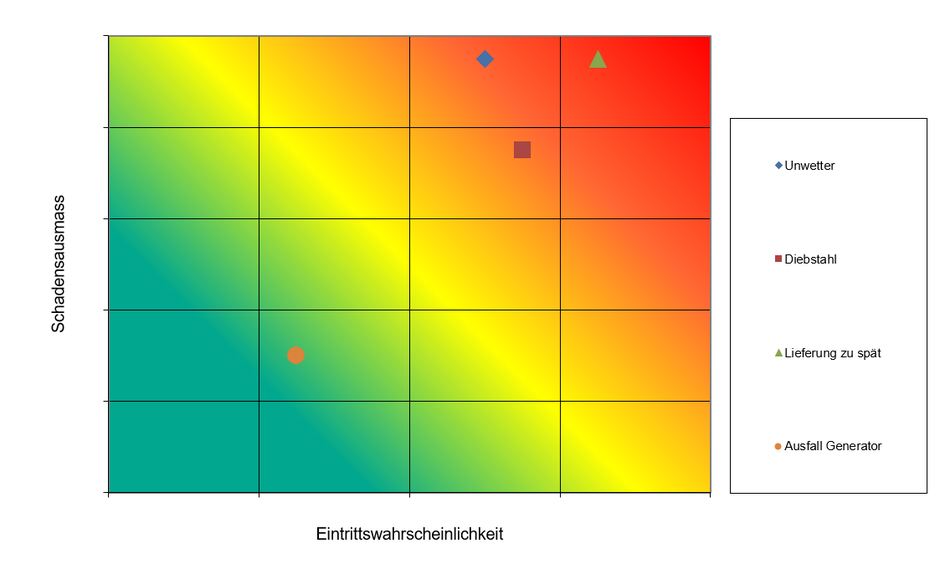
In der Praxis hat sich die Darstellung und Klassifizierung von Risiken offenkundig anhand der Risikomatrix (Riskmap) durchgesetzt. Schauen wir uns hierzu ein einfaches Beispiel an:

Risikomatrix MC FLO Excel Monte Carlo Simulation

Mit der Risikomatrix werden die Risiken in die Dimension «Eintrittswahrscheinlichkeit» (welche von links beginnend bei 0 anfängt und rechts mit 1 abschliesst) und «Schadensausmass» (beginnend mit 0 und endend entlang der vertikalen Achse mit dem maximalen Schaden) eingeteilt. Jedem Risiko wird ein Wert aus der Multiplikation der beiden Dimensionen zugewiesen.

Im obigen Beispiel werden die Risiken «Unwetter» und «Lieferung zu spät» im gleichen Rechteck (hohe Eintrittswahrscheinlichkeit und hoher Schadensausmass) abgebildet, während der Diebstahl mit gleich hoher Eintrittswahrscheinlichkeit aber gegenüber den anderen erwähnten Risiken geringerem Schadensausmass dargestellt ist. Was ist daran auszusetzen?*

Zum einen bedingt eine visuelle Darstellung eine Rangfolge der Einzelrisiken, damit gleichwertige Risiken sich nicht überlappen und somit die Grafik die Übersichtlichkeit beibehält. Dies kann jedoch zu Fehlinterpretationen führen.
Es gibt verschiedene Kombinationen von Eintrittswahrscheinlichkeit und Schadensausmass mit gleichem Erwartungswert; diese Fälle lassen sich aber nicht sachgerecht in ein Raster pressen.
Die Abbildung von Einzelrisiken ignoriert mögliche Korrelationen zwischen den Risiken.

Schauen wir uns den letzten Punkt genauer an und stellen wir uns vor, dass wir eine Fabrik betreiben und mögliche Unwetter einen Schaden (etwa durch fallendes Geröll) verursachen können. Es besteht das weitere Risiko, dass notwendige Teilelieferungen nicht fristgerecht bereit gestellt werden und somit ein weiterer Schaden entsteht. Beide Fälle sind als Einzelrisiken abgebildet. Aber kann es nicht sein, dass ein Unwetter sowohl einen Schaden an der Fabrik (vielleicht ein geringer) und gleichzeitig eine erhebliche Verzögerung bei der Teilelieferung, etwa durch umgestürzte Bäume auf dem Lieferweg, bewirkt? Ist es daher sinnvoll, dass die Risiken «Unwetter» und «Lieferung zu spät» als unabhängige Ereignisse aufgefasst werden sollen?

Wie in vielen anderen Blogs dargelegt, etwa unsere Ausführungen zum zentralen Grenzwertsatz, ist die Annahme unabhängiger Verteilungen - insbesondere im Kontext der Unternehmensführung und der damit verbundenen Risiken - nicht plausibel. Eine Risikomatrix sollte daher die Dimension der Abhängigkeit - welche durch Korrelationen zum Ausdruck gebracht werden kann - als wesentliches Merkmal aufführen.

Wie lässt sich dies konkret mit Zahlen begründen? Stellen Sie sich vor, dass Sie die Aufsicht von vier Projekten haben und Ihnen das Management den Auftrag erteilt hat, die Risiken in Zusammenhang mit diesem Portfolio und die Auswirkung auf die Rendite im Worst Case (etwa bei einer Schranke von 10%) darzustellen. Falls die Rendite hierbei unter 3% zu liegen kommen sollte, müsste das Management einschreiten und Massnahmen ableiten, um bei den geringeren Zahlungsrückflüssen die Tragfähigkeit des Unternehmens sicherzustellen.

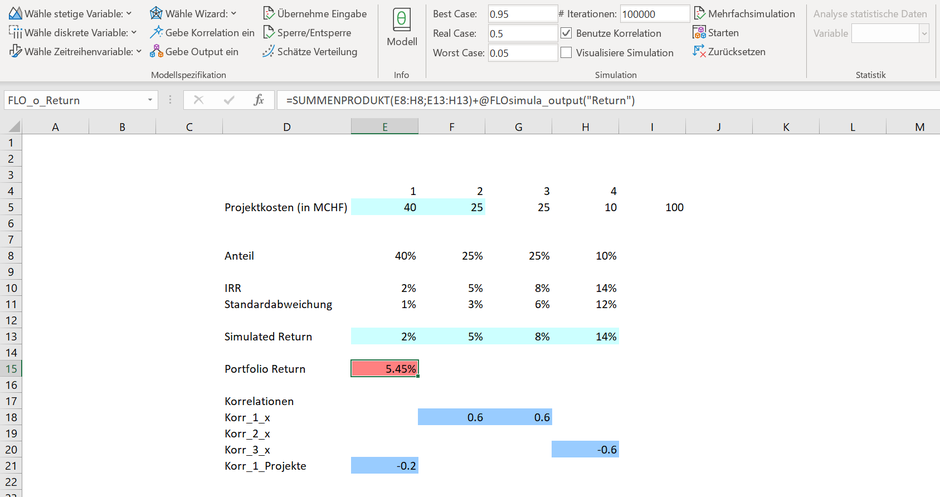
MC FLO Excel Monte Carlo Simulation Portfolio Rendite IRR Korrelation

Um das Ganze plastischer darzustellen, treffen wir die Annahme, dass das Portfolio aus dem Bau einer Autofabrikplattform (1) und der Produktion von 2 verschiedenen Modellreihen (2-3) auf dieser Plattform besteht (siehe Excel und Graphik), wobei die Korrelationen separat abgetragen sind. Eine positive Korrelation bedeutet, dass die Rendite der Modellreihen 2 und 3 steigen, wenn auch die Rendite der Plattform steigt (und umgekehrt). Vorstellbar sind Kosteneinsparungen in Zusammenhang mit der Plattform, welche sich in günstigere Produktionskosten und somit höheren Marktanteilen mit entsprechenden Renditen der Modellreihen 2 und 3 bemerkbar machen. Hingegen wird zwischen Modellreihe 3 und 4 eine negative Korrelation angenommen, was auf Kannibalisierungseffekte schliessen lässt (der Verkauf von SUV hat negativen Einfluss auf den Verkauf von Vans, welche auf eine anderen Plattform produziert werden; wir unterstellen bei allen Korrelationen eine Gauss/ Normalcopula).

Die vier Projekte weisen unterschiedliche Kosten und Erwartungen hinsichtlich der Rendite, ausgedrückt als IRR (internal rate of return) und deren Volatilität aus. Unter Berücksichtigung der Gewichtung der Einzelprojekte und deren mittleren Rendite wird ohne Simulation eine mittlere Portfoliorentabilität von 5.45% ausgewiesen.

Zwecks Aussage zur Risikosituation können die Projekte - analog oben - in eine Risikomatrix überführt werden, wobei das Schadenausmass durch die Volatilität bestimmt und deren Eintrittswahrscheinlichkeit durch die Dichtefunktion der unterstellten Normalverteilung abgeleitet werden. Hingegen kann mit der Risikomatrix keine Aussage darüber getroffen werden, wie die Risiken gesamthaft ausstrahlen und diese unter Berücksichtigung der Korrelationen auf das Portfolio wirken.

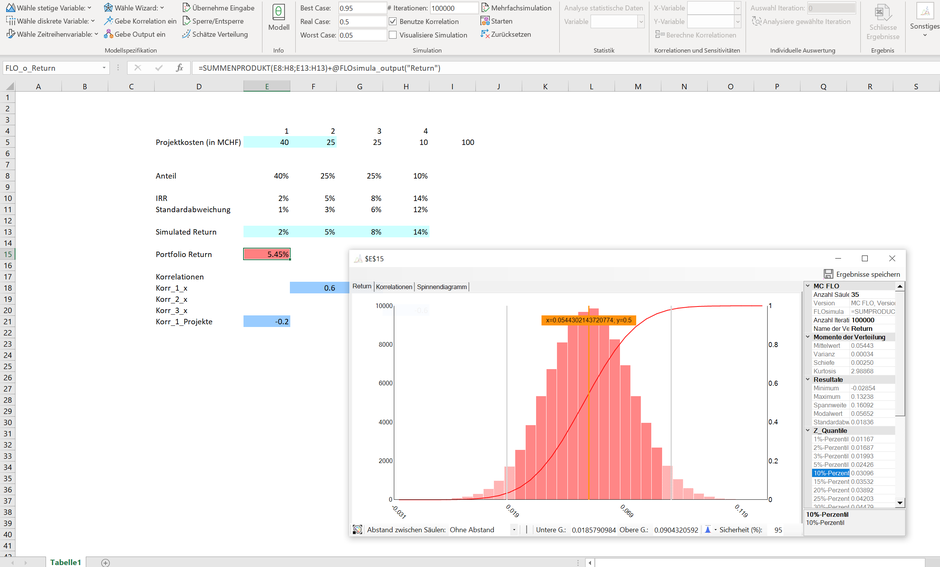
Eine Simulation mit 100'000 Iterationen ohne Berücksichtigung von Korrelationen zeigt eine Portfoliorendite von 2.7% im Worst-Case Fall auf (siehe 2. Bild unten, 10% Schranke rechts). Mit Berücksichtigung von Korrelationen beträgt die Portfoliorendite hingegen 3.1% und liegt somit über der kritischen Grenze (mittels Bootstrap wäre dieser Wert natürlich noch als Vertrauensintervall darzustellen).

Excel Monte Carlo Simulation Korrelation Risiken Risikomatrix

Während im ersten Fall zusätzliche Massnahmen eingeleitet werden müssten, kann unter Berücksichtigung der Korrelationen hingegen vorläufig eine Entwarnung ausgesprochen werden. Die Simulation deckt denn auch auf, was von vielen intuitiv als grösster Hebel empfunden wird: Wenn das erste Projekt (Rendite «r_1») ein Erfolg wird, dann werden die Folgeprojekte davon profitieren. Das lässt sich anhand von Plattformeffekten begründen. Die Simulation ohne die Berücksichtigung der Korrelationen zeigt jedoch nur den individuell grössten Hebel, hier die Rendite («r_3») des dritten Projektes auf. In diesem Fall würde das Management gar ein falsche Entscheidung treffen, wenn es allein Massnahmen zur Erhöhung der Profitabilität des dritten Projektes zu Lasten des ersten Projektes ergreifen sollte.

Um auf die einleitende Risikomatrix zurückzukommen: Wenn Sie schon an der Darstellung der Risikomatrix festhalten wollen, sollten Sie abhängige Risiken zu Clustern zusammenfassen und risikominimierende Massnahmen in Bezug auf Cluster definieren, nicht auf Einzelrisiken.

Bemerkung 1: Der IRR hat gegenüber anderen finanziellen Kennzahlen einige Nachteile, unter anderem, dass er nicht eindeutig ist. In Excel steht als Alternative der Modified Internal Rate zur Verfügung.

Bemerkung 2: Die hier unterstellte Herleitung der Portfoliorendite über eine Gewichtung und normalverteilter Renditen setzt implizit voraus, dass ein Markt für Projekte existiert und daher diese liquiditätswirksam zu jedem Zeitpunkt gehandelt werden können. Projekte haben aber eher den Charakter von (Real-)Optionen. Auch dies haben wir hier ignoriert.

Bemerkung 3 [02.05.2020]: Wir haben den Begriff des «Risikos» nicht einheitlich verwendet und in Bezug auf die Risikomatrix die gebräuchlichere Beschreibung angenommen.

* Siehe Gleissner, Romeike: "Die größte anzunehmende Dummheit im Risikomanagement - Berechnung der Summe von Schadenserwartungen als Maß für den Gesamtrisikoumfang", aufgerufen über http://www.werner-gleissner.de/publikationen-fachartikel-risikomanagement.php.

Risiken aus der Sicht eines Portfolios