Sie wollten schon immer Begriffe wie Vaue-at-Risk verstehen und dies in Excel ohne Mühe praktisch umsetzen? Dann los.
Gehen wir ans Eingemachte. Wir möchten den Value-at-risk eines Portfolios nach 10 Handelstagen bei einem Konfidenzniveau von 99% ermitteln, wobei das Portfolio aus den Titeln Gold und Silber zusammengesetzt ist.
Bevor wir die Kalkulation näher beschreiben, möchten wir Ihnen den Sinn des Value-at-Risk anhand einer einfachen Überlegung darlegen. Stellen Sie sich vor, dass Ihr Vermögen aus Wertschriften besteht und Sie in zehn Handelstagen den Kauf einer Firma planen. Den Kauf möchten Sie durch die Übertragung der Wertschriften tätigen. Damit der Partner mit einem guten Gefühl auf das Geschäft eingeht, möchte er sicherstellen, dass Sie am Transaktionstag über den notwendigen Gegenwert verfügen. Mit dem Value-at-Risk gemäss obiger Darstellung hat er eine Gewissheit von 99%, dass die Wertschriften nicht unter dem Verkaufspreis fallen.
Mit heutigem Tag wurde der Goldpreis mit US$ 1'289.2 und Silber mit US$ 17.11 per Feinunze gehandelt. Unser Portfolio besteht aus jeweils 500 Wertschriften pro Titel, womit ein Vermögen von US$ 653'155 resultiert (der Einfachhalt halber bleiben wir bei US$, kürzen dies aber auf $). Der Value-at-Risk kann alternativ wie folgt interpretiert werden: Wir möchten den Wert unseres Portfolios nach 10 Handelstagen ermitteln, bei dem noch eine "Wahrscheinlichkeit" von 1% besteht, dass dieser unter dem Value-at-Risk (VaR) fällt.
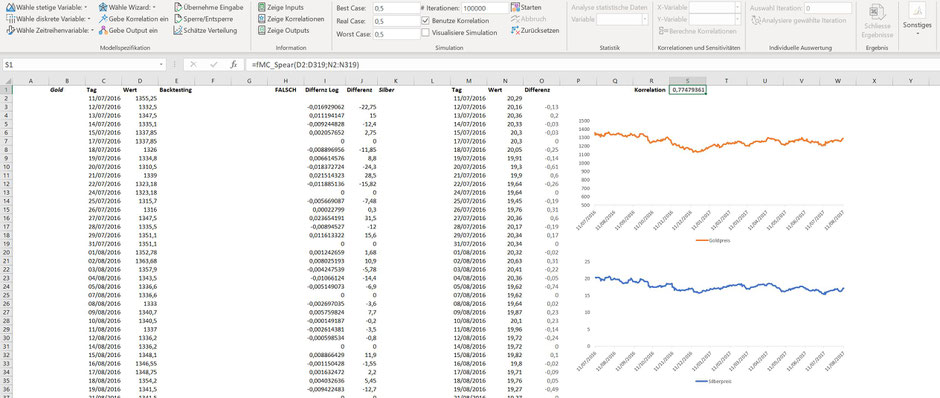
Um zur möglichen Antwort zu gelangen, müssen wir die Preise von Gold und Silber näher untersuchen. Unten sehen Sie die historische Entwicklung der beiden Titel über das untersuchte Handelsjahr. Das Modell können Sie hier nachvollziehen. Da Gold und Silber nicht immer gehandelt werden, haben wir die Tage mit fehlenden Daten aus der Datenbasis gefiltert. Auf dieser Basis haben wir dann die Korrelation (mittels des Ansatzes von Spearman) dieser beiden Titel ermittelt (0.77).
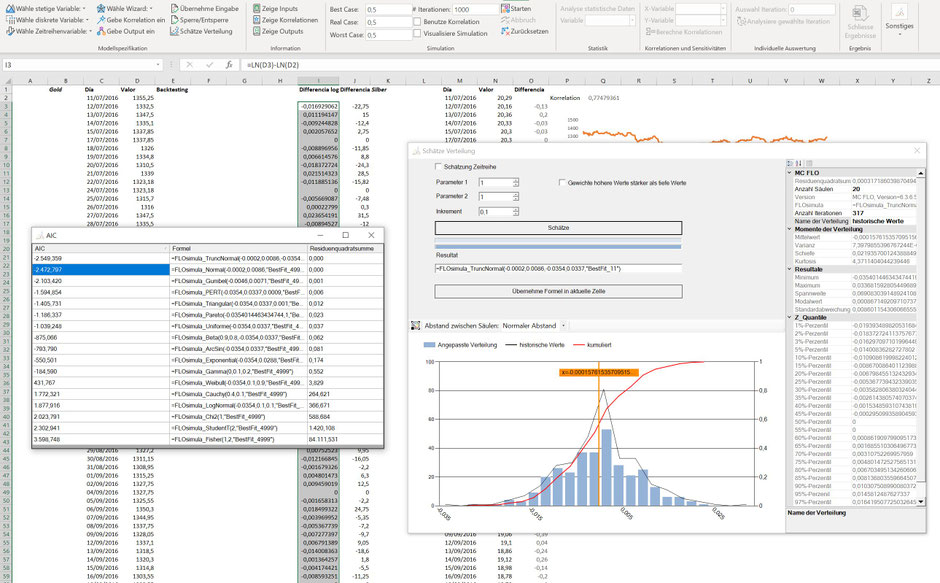
Im Nachgang haben wir die Preisentwicklung analysiert- zum einen direkt anhand der realisierten Preise und zum anderen anhand der logarithmierten Renditen. In beiden Fällen kommen wir zum Schluss, dass die Verteilungen nicht einer Normalverteilung folgen (die Kurtosis ist deutlich über 3), womit wir den Zeitprozess ARCH als Ausgangsbasis bilden wollen. Hierzu greifen wir auf die einfache Differenz zwischen den Preisen zwischen jeweils zwei Handelstagen auf, um den VaR zu bestimmen.
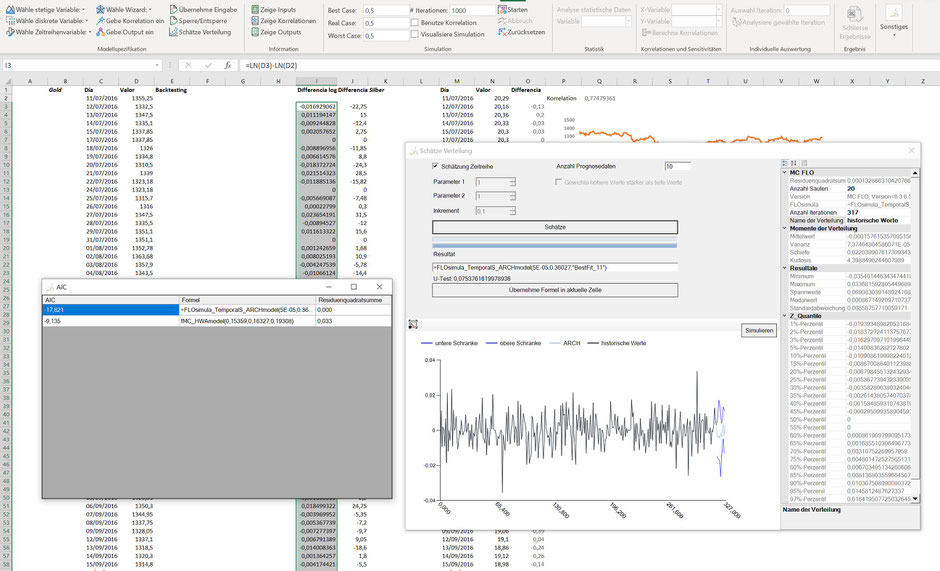
Hier sehen wir den ARCH Zeitreihenprozess, welchen MC FLO vorgeschlagen hat.
Unter der Annahme, dass die Zeitreihe nicht der Normalverteilung folgt, sind Aussagen zum möglichen Preis in der Zukunft nicht ohne Weiteres möglich, womit wir auf eine Simulation zur Bestimmung des VaR zurückgreifen. In der Praxis ist zudem häufig zu beobachten, dass mehrere Modelle herangezogen werden, was wir auch hier empfehlen. Neben dem ARCH (1) Modell für 10 Handelstage haben wir alternativ einen ARCH (1) Prozess mit einem Handelstag herangezogen und diesen dann mittels eines Quotienten auf 10 Handelstage hochgerechnet. In diesem Fall haben wir die Korrelation zwischen Gold und Silber berücksichtigt.
Da wir nicht in der Lage sind, die Hypothese der Normalverteilung zu 100% auszuschliessen oder alternativ den Beweis zu erbringen, dass das ARCH (1) Modell mit den definierten Parametern den wahren Prozess in Zukunft widerspiegelt, wird als Ergänzung eine Geometrisch-brownsche Bewegung (GBM) herangezogen.
So - nun können wir die Simulation starten, welche wir vorliegend mit 100'000 Iteration durchführen, was uns als genügend genaue Approximation erscheint.
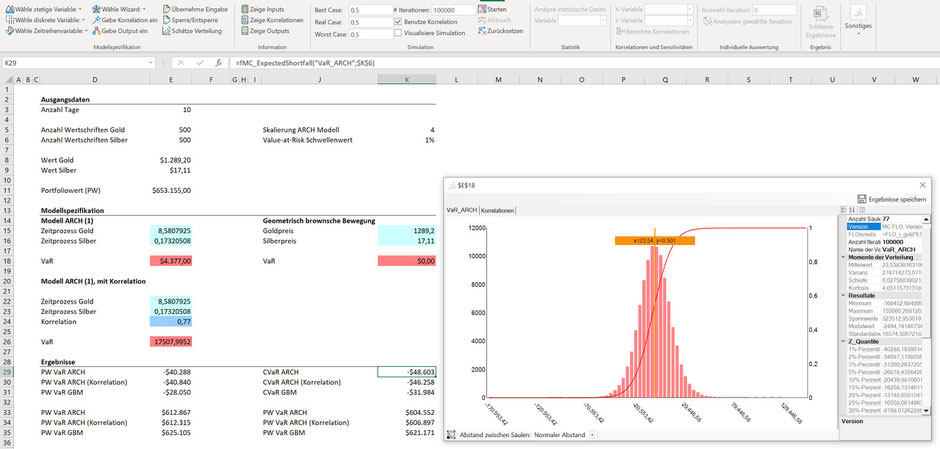
Hier sehen wir die Ergebnisse:
| Modell | VaR (99% Konfidenzniveau) |
| ARCH (1) | $ 40'288 |
| ARCH (1), mit Korrelation |
$ 40'840 |
| GBM | $ 28'050 |
Wenn wir den ARCH (1) Prozess als Massstab nehmen, kann der VaR auch wie folgt gedeutet werden: Es besteht eine "Wahrscheinlichkeit" von weniger als 1%, dass der Wert unseres Portfolios nach 10 Handelstagen unter $612'867 ($653'155 - $40'288) liegen wird, vom Tag der Bewertung an gerechnet. Oder anders: Wir haben eine Wahrscheinlichkeit von weniger als 1%, dass der Wert des Portfolios um mehr als $40'288 innert der nächsten 10 Handelstage fallen wird.
Um die einzelne Modelle zu überprüfen, haben wir diese einem Backtesting unterzogen, also den VaR für die historischen Daten berechnet. Es wurden dabei 193 Tage überprüft.
| Modell | Anzahl Fehler (in Prozent) |
| ARCH (1) | 0 (0%) |
| ARCH (1), mit Korrelation | 0 (0%) |
| GBM | 5 (2.59%) |
Das ARCH (1) liefert die besten Ergebnisse. Auf 193 Handelstage hat das GBM Modell hingegen an fünf Tagen einen VaR berechnet, welcher in der Realität unterboten wurde. Die Zielgrenze von 1% wurde - historisch betrachtet - somit nicht erfüllt, was jedoch - wie oben anhand der Verteilung der Daten ersichtlich - zu erwarten war.
Hingegen ist nicht der VaR die wesentlichen Grösse, sondern der erwartete Verlust, falls der VaR durchbrochen wird. Auf das Beispiel gemünzt: Wenn wir einen Verlust höher als $ 40'840 haben, wie hoch wird dieser im Durchschnitt sein? Diese Grösse haben wir als Conditional-Value-at-Risk festgehalten (CVaR), oder auch Expected Shortfall.
Mit der in MC FLO eingebauten Funktion zum Expected Shortfall ist die Ermittlung dieser Grösse ein Kinderspiel.
| Modell | CVaR (bei 99% Konfidenzniveau) |
| ARCH (1) | $ 48'603 |
| ARCH (1), mit Korrelation | $ 46'258 |
| Wiener Prozess | $ 31'984 |
Das Ergebnis lässt sich sodann wie folgt interpretieren: Im Fall, dass der VaR durchbrochen wird, beträgt der mittlere Verlust beim ARCH (1) Modell $ 48'603 oder anders ausgesprochen: Das Portfolio wird beim Durchbrechen des VaR im Mittel bei $605'051 zu liegen kommen.
Falls der Verkaufspreis bei $600'000 liegt, wäre beim VaR Ansatz mit einem Ausfall von unter 1% zu rechnen (dies natürlich unter der Annahme, dass es zwischenzeitlich keinem gelingen sollte, Gold und Silber quasi aus dem Nichts zu erschaffen). Und auch wenn der VaR durchbrechen werden sollte, ist im Schnitt mit einem Portfoliowert zu rechnen, welcher den Verkaufspreis übersteigt.
Die Hinterlegung der Wertschriften als Tauschobjekt ist daher in diesem Fall mit geringen Risiken verbunden.

Kommentar schreiben