Benutzerdefinierte Verteilungen – ein Exkurs

In der Praxis werden benutzerdefinierte Verteilungen oftmals den klassischen Verteilungstypen (wie die Normalverteilung) in der preskriptiven Analyse mittels Simulationen vorgezogen. Es mag wohl daran liegen, dass Letztere idealisierte Verteilungen reflektieren und in der Praxis keine oder nur eine ungenügende Annäherung an die tatsächlichen Sachverhalte darstellen.

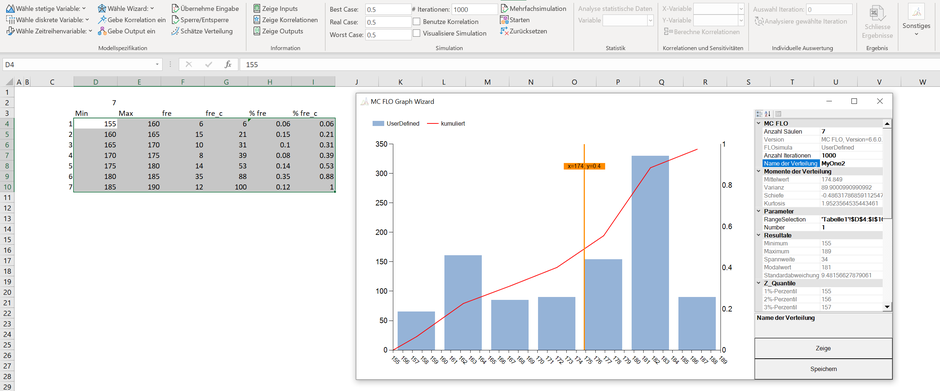
Mit MC FLO stehen drei Methoden zur Generierung von benutzerdefinierten Verteilungen zur Verfügung. Die erste besteht darin die Daten direkt - welche im Excel zusammenhängend in Zellen vorliegen – einzulesen. Folgende Darstellung zeigt das Ergebnis des Einlesens und der anschliessenden Simulation mit 1'000 Iterationen. Hierzu brauchen Sie in MC FLO nur die Zellen zu markieren und über «Wähle Wizard» -> «Benutzerdefinierte Verteilung» erscheint im Nu das Ergebnis.

Durch Anpassung der Anzahl «Säulen Säulen» im Histogramm kann als Erweiterung eine Verfeinerung oder Aggregierung der Daten – je nach Fragestellung – vorgenommen werden.

Als zweite Möglichkeit ist die Ausarbeitung eines geeigneten Histogramms zu nennen, welches vor allem bei Expertenbefragungen zum Tragen kommt.

Stellen wir uns vor, dass wir die Verteilung von Frauen und Männern unserer Sportclubs nach der Körpergrösse abbilden möchten. Wir kennen die Grösse der einzelnen Mitglieder nicht, sondern möchten allein aufgrund unserer Intuition eine Verteilung herleiten. In einem ersten Schritt treffen wir Annahmen über den geringsten und den höchsten Wert: Sagen wir, dass davon ausgegangen werden darf, dass die kleinste Person eine Körpergrösse von 155 cm und die grösste Person eine solche von 190 cm aufweist. Wir möchten – aus Vereinfachungsgründen – die Körpergrösse in 7 Intervalle aufteilen.

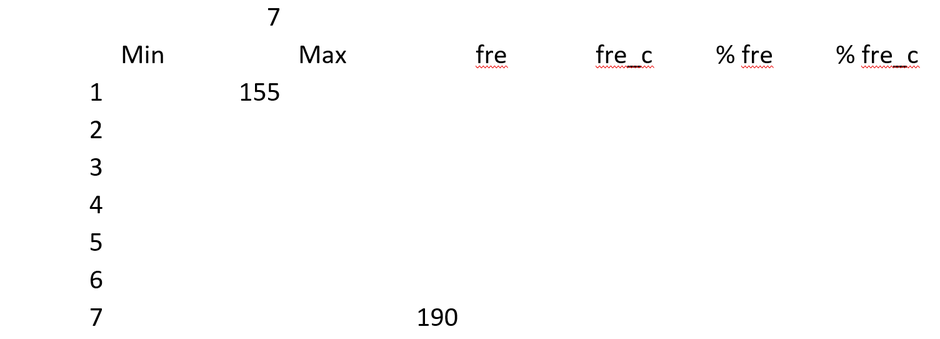
Wir erstellen ein Grundgerüst für ein Histogramm, in der das Minimum und das Maximum eingetragen werden. Die Anzahl (fre), die kumulierte Anzahl (fre_c), der Prozentwert der Anzahl an der Grundgesamtheit (% fre) und dessen kumulierte Anzahl (% fre_c) lassen wir zuerst leer.

Da wir eine Intervallgrösse von 7 gewählt haben (es könnten auch 10 oder 3 sein), können wir die Spannweite der Intervalle einfach errechnen: (190 – 155) / 7 = 5 und anschliessend die Min und Max Zahlen über alle 7 Intervalle befüllen:

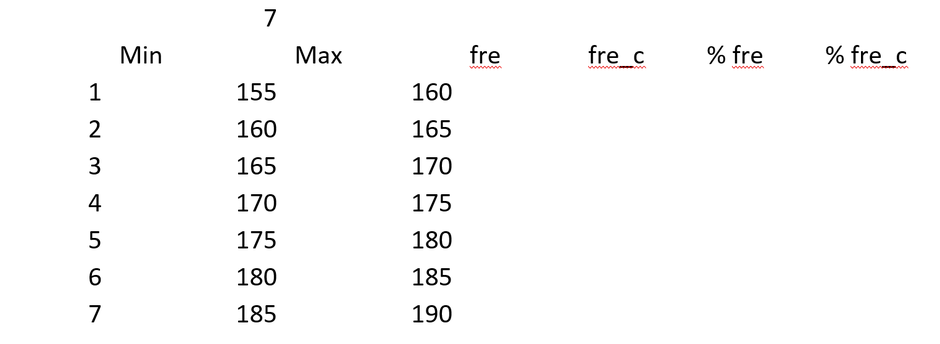
Wir wissen, dass 100 Personen im Sportclub sind, wovon ca. 70% auf Männer entfallen. Ab hier können zwei Strategien verfolgt werden: Zum einem können wir die Anzahl Personen schätzen, welche auf das jeweilige Intervall entfallen. Wir könnten uns also fragen, wie viele Personen zwischen 155 cm und 160 cm gross sind und dies unter «fre» eintragen. Alternativ können wir die Verteilung der Grösse von Frauen und Männern separat schätzen und diese dann in die Intervallgrenze überführen. Wir wählen die zweite Strategie. Wir befragen die Experten nach der durchschnittlichen Grösse der Männer und der Abweichung hiervon. Gehen wir davon aus, dass die durchschnittliche Grösse mit 184 cm angenommen wird und 35 Männer im Intervall 6 (180-185 cm) davon betroffen sind. Für die weiteren 35 Männer (in Summe somit 70) wird folgende Verteilung vorgeschlagen:

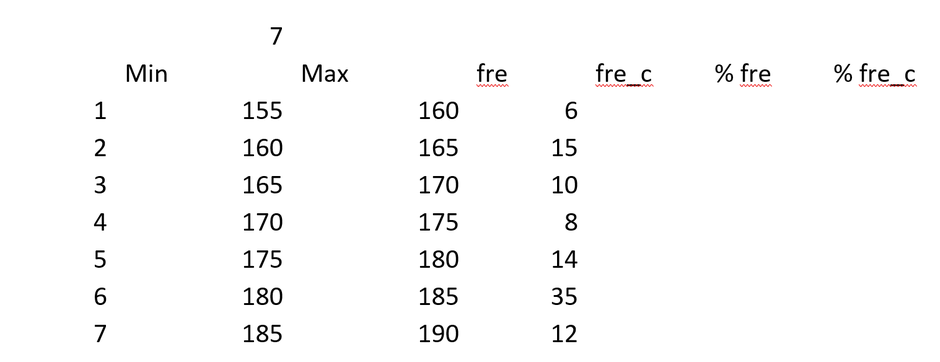
Die Experten schätzen somit, dass 4 Männer eine Körpergrösse zwischen 165 cm und 170 cm aufweisen. Analog können wir beim 30% Anteil der Frauen vorgehen.

Jetzt müssen wir noch die einzelnen Werte bei «fre» addieren und schon haben wir die Verteilungsannahme anhand der Expertenschätzung vorliegen.

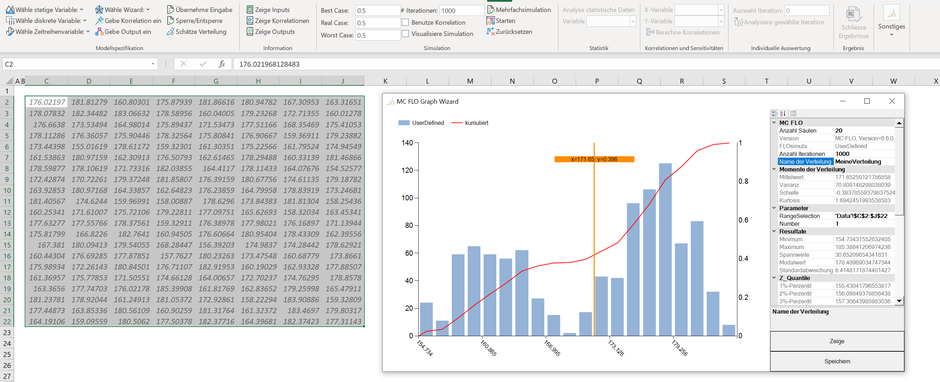
Als letzter Schritt sind die anderen relevanten Grössen einzutragen. Falls Sie nicht genau wissen, wie diese Zahlen aufzubereiten sind, können Sie sich an dem mit MC FLO beigelegtem Beispiel orientieren. Markieren Sie die Daten und über «Wähle Wizard» -> «Benutzerdefinierte Verteilung» kann das Histogramm nun eingelesen werden. Abschliessend tragen Sie den Variablennamen unter «Name der Verteilung» ein und speichern die Verteilung in einer leeren Excelzelle ab. Sie können - analog oben - die Variable nun für eine Simulation als Inputvariable verwenden.

Die dritte Möglichkeit macht sich der Flexibilität von MC FLO und Excel zunutze: Excel schert sich nicht darum, ob eine Variable als Output oder als Input definiert wurde und MC FLO hat kein Problem damit, eine Outputvariable wiederrum als Input für eine andere Variable zu verwenden.

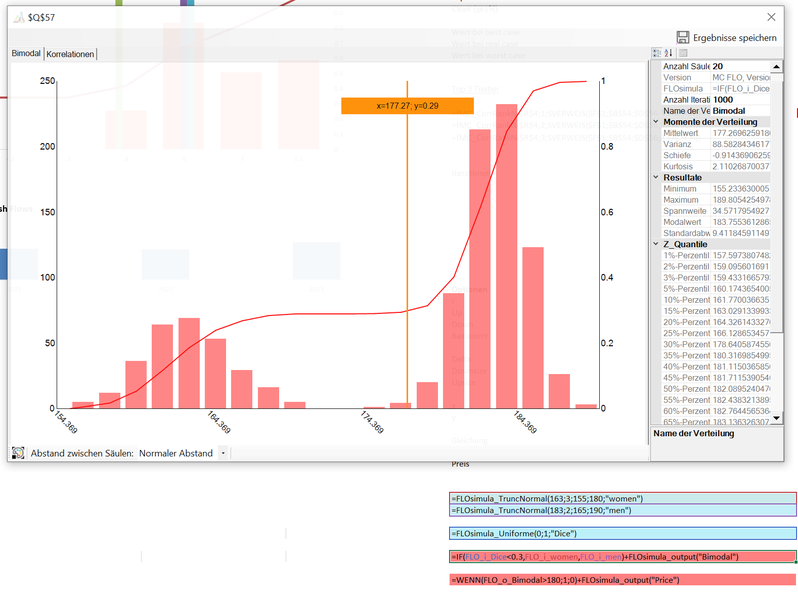
Für die Bestimmung des Grössenproblems können wir uns zwei gekappte Normalverteilungen vorstellen, eine welche die Verteilungen der Frauen («women») und die andere, welche die Verteilungen der Männer («men») beschreibt. Des Weiteren brauchen wir eine Variable, welche das Verhältnis der Männer an der Grundgesamtheit des Sportclubs widerspiegelt. Wir können dies durch eine Bernoulli-Verteilung oder durch eine Gleichverteilung («dice») darstellen, was wir hier vorliegend gemacht haben. In der Outputvariablen ("Bimodal") haben wir dann beide Verteilungen zu einer neuen Verteilung zusammengefügt. Diese Variable können wir wieder als Input im Modell verwenden.

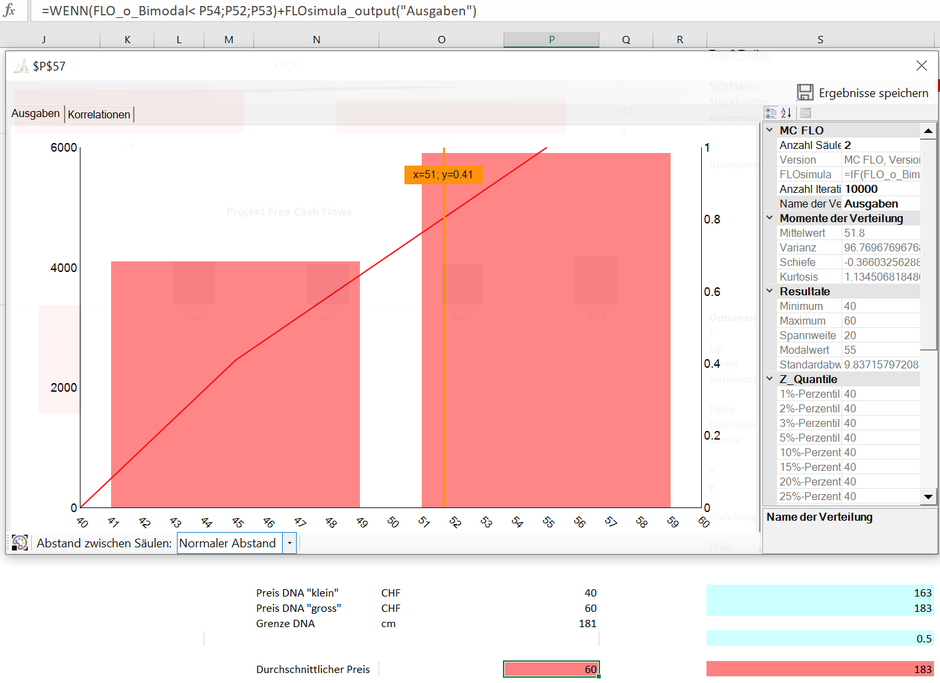
Stellen wir uns vor, dass (sehr fiktiv) ein DNA Test von der Körpergrösse abhängt und wir die durchschnittlichen Kosten dieses Tests berechnen wollen. Eine Simulation mit 10'000 Iteration mit der benutzdefinfierten Verteilung zeigt auf, dass die durchschnittlichen Kosten bei 51.8 CHF pro erwachsener Person liegt.

Die Definition von benutzerdefinierten Verteilungen in MC FLO ist in Kombination mit Excel ein Kinderspiel. Durch den Rückgriff auf verschiedene Techniken können Sie je nach Erfahrung und Expertenwissen ein massgeschneidertes Instrument bereitstellen.

P.S.: Das Abstützen auf eine Outputvariable hat einen kleinen Schönheitsfehler, da MC FLO nur die Korrelation zwischen Inputvariablen erlaubt. Möchten Sie Korrelationen im Modell verwenden, können Sie in einem ersten Schritt eine Simulation für die Outputvariable vornehmen, das Ergebnis hiervon (etwa das von 1'000 Iterationen) abspeichern und die Daten - wie oben als erste Möglichkeit beschrieben - zur Bestimmung einer benutzerdefinierten Verteilung wieder heranziehen. Clever, nicht wahr?