The Perplexing Math of Uncertainty – A reply

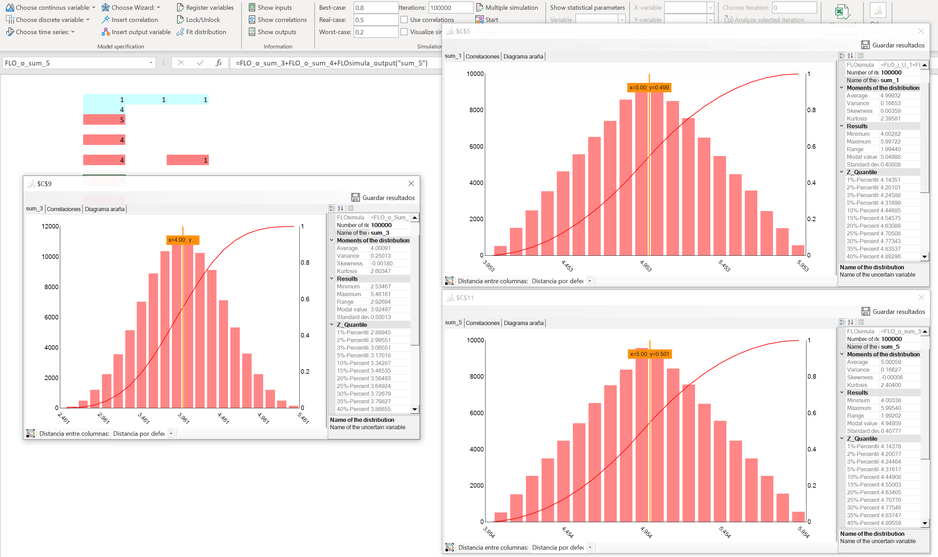
In the seminal paper “The Perplexing Math of Uncertainty” by David Vose the author states that subtraction should be avoided whenever the result value "C" incorporates some of the input values. To underline his assertion, the author begins by adding two independent uniform variables, A(0.5, 1.5) und B(3.5, 4.5), to obtain a triangle distribution C(4,6,5), called "sum_1", see the image at the end. In the next step the author subtracts from C another random variable with the same distribution as A (called A’(0.5, 1.5)). The result is approximately normal distributed (with mean 4 and standard deviation of 0.5, N(4,0.5), see "sum_3") and therefore not B.

From this we can conclude that

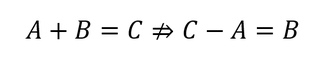
or

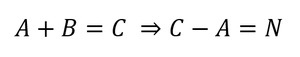
using C as a well behaved (with mean and variance) triangular distribution, and A and B defined as uniform distributions. 

However, how do we know that only A and B determines C? Is there perhaps another variable – with uniform distribution as A –, such that adding N to it yields our result C? So we ask:

Is it possible to add A to two different distributions, so that following equalities hold?

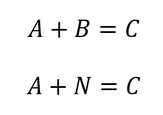
We define A’’ as the mirror image of A, or in this case A’’ = 2 – A (if A takes the value 0.5, A’’ takes the value 1.5). As A is uniform distributed, the mirror image will also be uniform distributed within the same ranges. Using a simulation and adding A’’ to N gives our expected result C(4,6,5), see "sum_5". This confirms that neither adding nor subtraction under uncertainty is unambiguous. Traditional mathematics states that equality “3 + x = 5” holds only if x = 2 (or, if we add 3 and 2 we’ll get only 5), however under uncertainty a unique solution is not guaranteed. Or in other terms: If we subtract A from C we get in our case two feasible solutions.

So, the authors claim is true, if and only if we have prior knowledge of the distributions A and B.

We conclude that subtraction is a valid operation under uncertainty – we should however take in mind, that the resulting distribution is not necessarily the only feasible solution.

Note: The calculations have be performed using the English version of MC FLO with Spanish characters enabled.