MC FLO kann mit Recht als das mit am Markt schlankeste Programm für Monte-Carlo Simulationen auf Basis von Microsoft Excel für Windows bezeichnet werden. Und dies bei umfangreichen Funktionsumfang (Copulas, Zeitreihen, Verteilungsanpassung, Bootstrapping etc.).
Trotzdem sind auch bei MC FLO Abstriche in Kauf zu nehmen. So werden Unter - und oder Obergrenzen explizit nur bei der Normalverteilung unterstützt. Wie Sie solche trotzdem für Verteilungen (etwa Dreieck, PERT) berücksichtigen können, erfahren Sie hier. Gängige Risk-Sharing Modelle, welche im Anschluss präsentiert werden, greifen auf Unter - und Obergrenzen glücklicherweise nur implizit zurück.
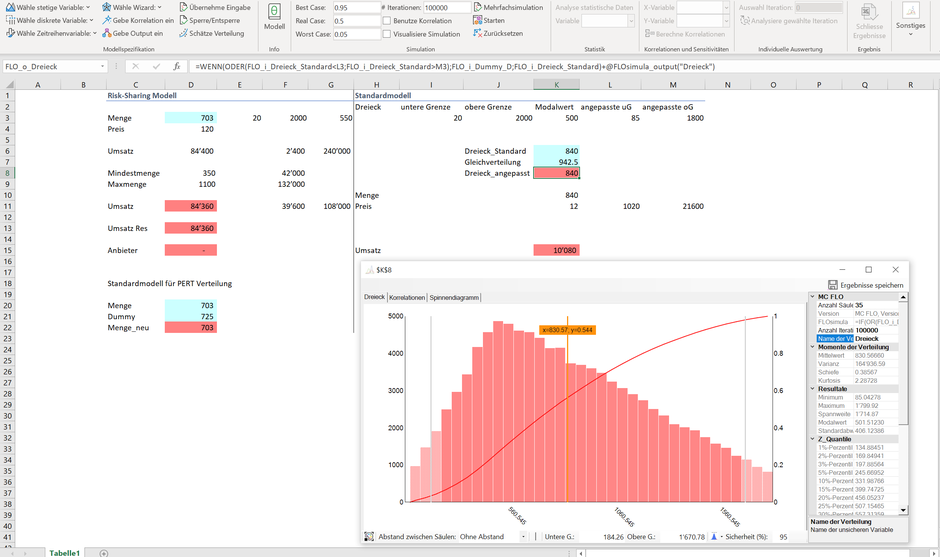
Beginnen wir mit einem einfachen Modell. Auf der rechten Seite haben wir in Spalte I bis K eine Dreiecksverteilung mit den entsprechenden Parametern abgebildet. Die untere Grenze liegt bei 20, die obere Grenze bei 2'000 und der Modalwert bei 500. Wir können uns diese Verteilung als Nachfrage nach einem Gut vorstellen. Ein Anbieter wird diesen Markt nur dann bedienen wollen, wenn die Nachfrage mindestens 85 und die maximale Nachfrage bei 1'800 liegt (etwa aufgrund von Kapazitätsrestriktionen). Wir nehmen an, dass der Anbieter zu beliebiger Zeit die Produktion des Gutes ohne Folgekosten sicherstellen kann (zu denken ist etwa an ein Food-Truck, der die Nachfrage nach Take-Away Essen über eine Onlineplattform überblicken kann). Für den Anbieter ergibt sich die Nachfrage somit als Dreiecksverteilung mit den Untergrenzen von 85 und 1'800. In Zelle K6 haben wir die ursprüngliche und in Zelle K8 die angepasste Dreiecksverteilung als Outputvariable abgetragen. Letztere greift auf eine Gleichverteilung mit den Grenzen 85 und 1'800 zurück. Bei einem angenommen Absatzpreis von 12 Euro pro Einheit kommen wir mit einer Monte-Carlo Simulation auf einen erwarteten Umsatz von knapp 10'000 Euro. Dies unter der Voraussetzung, dass die Nachfrage in der Betrachtungsperiode über 85 Einheiten liegt.
Das Heranziehen einer Gleichverteilung mit den erwarteten Grenzen kann für jede Verteilung (etwa Gumbel oder Fréchet) zur Bestimmung von Unter - und Obergrenzen herangezogen werden. Im praktischen Kontext ist eine explizite Herleitung der Unter - und Obergrenzen jedoch kaum üblich. Vielmehr werden implizite Unter - und Obergrenzen bei der Problemlösung herangezogen. Hiermit sind wir beim Risk-Sharing.
Ausgangslage von Risk-Sharing Modellen bildet das quantitative Risikokonzept, welches positive und negative Abweichungen vom Erwartungswert als Risiko qualifiziert. Soll das Risiko (Volatilität) für den Halter reduziert werden, kann dies durch Abtretung der Risiken mittels Vertrag an einen Dritten erfolgen. Dieser wird durch die Risikoübernahme eine Prämie verlangen.
Im Gegensatz zum ersten Modell haben wir nun die Nachfrage nach einem Gut als PERT Verteilung modelliert, mit einer Untergrenze von 50 und einer Obergrenze von 2'000 Einheiten pro Periode. Der Modalwert liegt bei 550 Einheiten (Spalten D-F). Stellen wir uns vor, dass das Gut eine Vorleistung - etwa eine Komponente für die Automobilbranche - darstellt. Bei einem angenommenen Preis von 120 Euro pro Einheit resultiert ein Mindestumsatz von 2'400 Euro (bei 50 Einheiten) und ein Maximalumsatz von 240'000 Euro (bei 2'000 Einheiten) pro Planungsperiode (siehe Zelle F8 und F9).
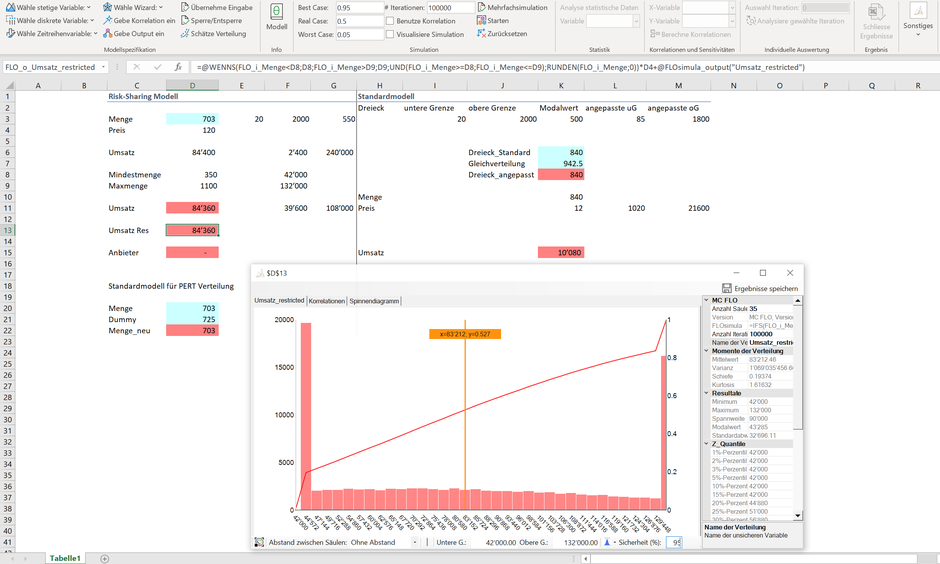
Der Zulieferer ist risiko-avers und möchte die Transaktionskosten bei mangelnder Liquidität minimieren. Er bietet dem Autohersteller folgenden Deal an: Falls die Nachfrage unter 350 Einheiten fallen sollte, dann übernimmt der Hersteller den Umsatzverlust, andernfalls und falls die Nachfrage über 1'100 Einheiten beträgt, dann bekommt der Hersteller die Differenz zu den 1'100 Einheiten unentgeltlich zur Verfügung gestellt. Für den Zulieferer beträgt der Mindestumsatz neu 42'000 Euro und der Maximalumsatz ist auf 132'000 Euro pro Periode beschränkt. Durch den Mindestumsatz stellt der Zulieferer sicher, dass auch in Krisenzeiten das Unternehmen über genügend Liquidität verfügt und somit den Mitarbeitern die Löhne ausbezahlen kann.
Umgekehrt muss der Hersteller dem Zulieferer bei einer geringen Nachfrage höchstens 39'600 Euro (42'000 - 2'400 Euro) bezahlen, hat aber im besten Fall einen Gewinn von 108'000 Euro (240'000 - 132'000 Euro). Soll der Hersteller auf dieses Risk-Sharing Angebot eingehen?
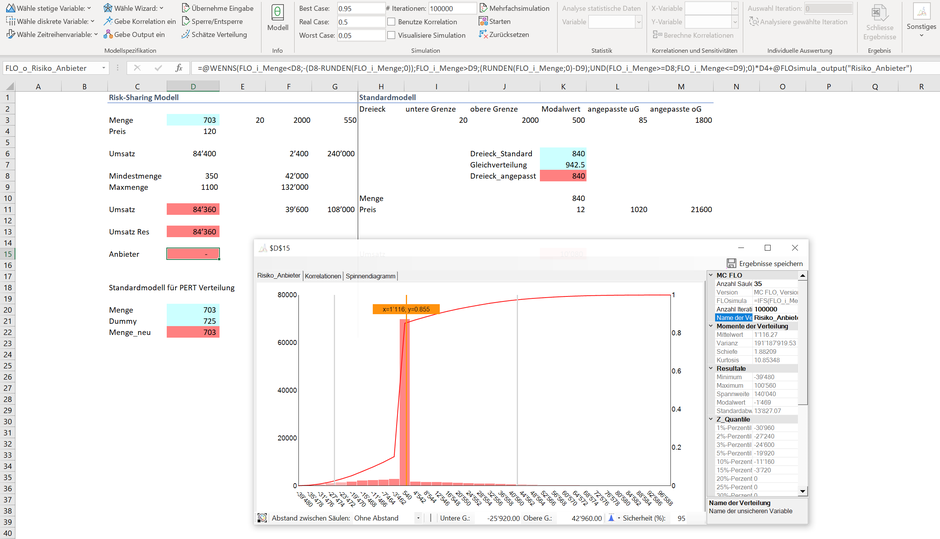
In Zeile D13 ist die Umsatzverteilung des Zulieferers und in Zelle D15 die Zahlungsmatrix des Automobilherstellers abgebildet. Die Werte aus der Simulation erscheinen mittels Klick auf die entsprechenden Zelle. So sehen wir, dass der Erwartungswert für den Zulieferer weiterhin knapp 84'000 Euro beträgt, dies trotz Risikoüberwälzung.
Für den Automobilhersteller beträgt der Gewinn aus dem Deal knapp 1'100 Euro (siehe Mittelwert oder magischer Strich) und ist somit positiv. Falls die Transaktionskosten geringer als 1'100 Euro ausfallen, dann ist der Deal gerade noch vorteilhaft. Mit dem Risk-Sharing Modell ist beiden Seiten gedient: Der Zulieferer bekommt einen Mindestumsatz zugesprochen und der Hersteller ist froh, dass er den kompetenten Zulieferer weiterhin als Partner hat.
Risk-Sharing Modelle verzerren - wie oben gesehen - keine Erwartungswerte und können nicht allein unter dem Blickwinkel der Covid-19 Krise zu einer Mitigation der Folgen bei einer Pandemie führen. Dies bedingt aber, dass Unternehmen ökonomische Gewinne in guten Zeiten zu Gunsten einer Risikoabsicherung in schlechten Zeiten abtreten müssten. Trotzdem: für ein potentielles Versicherungsunternehmen, welches die Risiken trägt, dürfte es nicht ein Einfaches sein die Prämie zu bestimmen. Die Covid-19 Krise ist systemisch und betrifft nahezu alle Branchen, was den Diversifikationseffekt relativiert. Erschwerend kommt hinzu, dass die Risikowahrnehmung zwischen den Vertragspartnern aufgrund asymmetrischer Informationen oftmals nicht kongruent ist, was eine Preisfindung erschwert.

Kommentar schreiben