Unsicherheit, ein beklemmendes Gefühl? Eine Reflektion über die Unternehmensplanung mit Simulationen

In den vielen Diskussionen, welche wir in den letzten Wochen geführt haben, sind uns immer wieder Gefühle der Ohnmacht entgegengebracht worden, welche mit der Planung eines zukünftigen Ereignisses in Verbindung gesetzt werden. Auslöser ist natürlich das Drama rund um Covid-19. Bei aller Bestürzung um die persönlichen Schicksale untermauert Covid-19 eine uns bereits bekannte Tatsache: Die Zukunft ist unsicher und wird es wohl immer bleiben. Und auf die Frage welche Planwerte in Zukunft einzustellen sind, entgegen wir im gleichen Atemzug, dass dies eine vom Management zu treffende Entscheidung ist. Das kann keine Statistik oder Mathematik gänzlich abnehmen. Wir betonen jedoch stets, dass die traditionellen Methoden der Planung, das Beiziehen von Punktwerten statt Bandbreiten, niemals gegriffen haben und auch zukünftig noch weniger einen Erkenntnisbeitrag leisten können*.

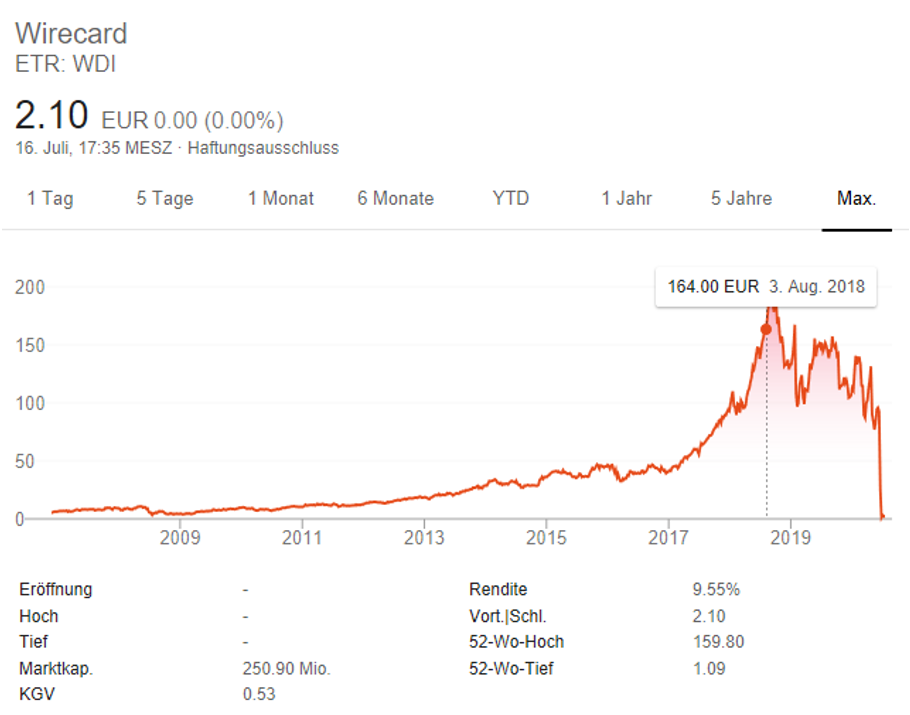
Des Weiteren geben wir weiter, dass mit dem Fortschreiben des Trends anhand von Zeitreihenmodellen grosse Vorsicht geboten ist, da diese Modelle den Blick in die Zukunft nur über den Rückspiegel – auf Basis bereits eingetretener Daten – ermöglichen. Ganz nach dem Motto: Was in der Vergangenheit nicht eingetreten ist, wird sich folglich in Zukunft nicht einstellen. Wenn dem so wäre, läge die Aktie von Wirecard (Stand Juli 2020) auf Basis der Daten bis Anfang August 2018 so stark im Plus, dass sich in der folgenden Graphik kein Platz zur Darstellung fände.

Den heutigen Stand kennen wir.

Wir stehen für einen Ansatz, bei der die möglichen zukünftigen Zustände systematisch – durch Analyse der Prozesse und der davon ausgelösten Auswirkungen – betrachtet und simuliert werden. Dies setzt voraus, dass die Zustände quantifiziert und innerhalb einer Bandbreite unter Angabe einer Wahrscheinlichkeitsverteilung anzugeben sind. Was auf den ersten Blick komplexitätssteigernd** wirkt, entpuppt sich bei konsequenter Umsetzung als wesentliche Hilfestellung bei der Entscheidungsfindung, da nur eine Simulation sinnvoll aufdecken kann, welche Treiber das gesuchte Ergebnis – bei allen möglichen Variationen - am stärksten beeinflussen und welche nicht.

Der Beizug einer Simulation bedeutet dabei nicht, dass alle Prozesse und Abhängigkeiten in Tiefe zu durchdringen sind. Bewährte Prozesse, welche auch zukünftig Bestand haben sollen, können durch datengetriebene Verfahren – wozu die Monte-Carlo Simulation auch gehört (siehe Blog zu Data Mining) – weiterhin angesetzt werden***. Durch die Übernahme der Daten in eine Verteilungsfunktion mittels Verteilungsanpassung oder direkter Verwendung dieser Daten und unter Berücksichtigung der Abhängigkeiten («Korrelationen») können verschiedene Konstellationen umfassend betrachtet und der Zeitaufwand der Planung in Grenzen gehalten werden.

Wir wissen natürlich auch, dass die Gretchenfrage, welche Verteilungsfunktion konkret - etwa zu Marktanteilen bei der Lancierung eines neuen Produktes anzusetzen ist - nicht einfach zu beantworten ist. Auch ist uns bewusst, dass nur selten eine Überprüfung der Verteilungsannahme ex-post möglich ist. So können wir gegen Ende des Jahres nur die Gesamtnachfrage (oder den Marktanteil) beobachten, nicht aber deren Verteilung. Wenn wir beispielweise unterstellt haben, dass die Nachfrage gleichverteilt zwischen 10'000 und 20'000 Einheiten schwankt und am Ende des Jahres 18'000 Einheiten verkauft wurden, dann können wir festhalten, dass die verkauften Einheiten innerhalb des Planungskorridors zu liegen kamen, nicht aber, ob eine Beta-Verteilung (mit alpha und beta <> 1) eine bessere Verteilungsannahme gewesen wäre. Dieser Sachverhalt – die fehlende ex-post Beobachtung planerischer Daten zur Festlegung der «a posteriori» Verteilung - wird oftmals von den Kritikern einer Monte-Carlo Simulation hervorgebracht, da kritische Berechnungen – wie etwa der Value-at-Risk – wesentlich verzerrt sein können. Es ist in der Tat etwas anderes, wenn der Value-at-Risk bei 99% Sicherheit nur bei ca. 10'100 (bei unterstellter Gleichverteilung) oder bei ca. 13'500 (bei unterstellter Beta-Verteilung [alpha=6, beta=2]) Einheiten eingeordnet wird. Diese Kritik ist berechtigt, lenkt aber davon ab, dass a) der Beizug einer Monte-Carlo Simulation nicht zur Elimination der Unsicherheit führt, noch von den Befürwortern einer Simulation entsprechend formuliert wird und b) die einwertige Planung nicht besser aufgestellt ist. Schlimmer noch: die einwertige Planung ist nicht in der Lage überhaupt eine Aussage zum Value-at-Risk – um nur eine «at risk» Kennzahl zu nennen – machen zu können****.

Der Vergleich kann wie folgt vorgenommen werden: Die Punktplanung gibt zwei Punkte vor (die letzte beobachtete Zahl, etwa das letzte Jahresergebnis und das neue Jahresergebnis), legt aber nicht dar, wie der Weg von dem einen Punkt zum anderen ist, noch ob der Plan «ambitioniert» ist. Die Simulation zeigt hingegen die möglichen Wege auf, ist aber unscharf in der Frage, ob die Wege eher breit oder doch schmal sind.

Wir halten fest: Wenn Sie eine Planung auf Basis von Simulationen aufsetzen, seien Sie sich bewusst, dass die Unsicherheit nicht eliminiert ist und Sie in weiten Teilen auf Basis von Annahmen die Planung gestalten müssen. Im Gegensatz zur «einwertigen» Planung haben Sie aber mit der Simulation das richtige Instrument in der Hand, um auf Basis von nachvollziehbaren Zahlen und unter Einschluss der Wechselwirkungen von Geschäftsprozessen eine bessere Entscheidung treffen zu können.

*Wer Punktwerte plant, sollte auch daran gemessen werden. Oder anders: Wer den Punkt nicht trifft, hat beim Planen versagt.

**Eine Simulation ist rein methodisch nie komplexitätssteigernd, da die Unsicherheit Bestandteil nahezu sämtlicher unternehmerischer Handlungen ist. Simulationen führen hingegen zu einer Komplexitätsverlagerung: von den Köpfen einzelner Manager in ein nachprüfbares Rechen-/ Modellwerk.

***Ein im Audit/Compliance bekanntes Verfahren zur Entdeckung von Fehlverhalten ist die Anwendung des Benfordschen Gesetzes, welches wie Simulationen eine Verteilung heranzieht. Demnach hätten Manipulationen in der Bilanz von Wirecard wohl früher entdeckt werden können.  

****Verteilungsfunktion lassen sich aber durchaus aggregiert zusammenstellen: So können Sie zu allen Marktneulancierungen aus der Vergangenheit die Marktanteile erfassen. Wenn die Marktanteile und davon abgeleitet die Nachfrage einer Gleichverteilung folgen, dann sollten Sie diese als «a priori» als auch als «a posteriori» Verteilung für die nächste Neulancierung ansetzen. Und: Da wir ex-post für einen konkreten Geschäftsfall weder eine Gleichverteilung noch eine Beta-Verteilung beobachten können, ist die «Verzerrung» des Value-at-Risk rein theoretisch. Es bleibt ein unternehmerischer Entscheid unter Unsicherheit.