In der mit MC FLO mitgelieferten Beispieldatei wird das Verfahren der Markow Kette konkret am Rating von Unternehmen demonstriert. Wer sich nach der genaue Definition von Markow Ketten in gängigen Internetforen erkundigt, wird auch rasch fündig. Vereinfacht kann ein Markow-Prozess so zusammengefasst werden: Bei der Markow Kette handelt sich um einen zufallsbedingten Prozess, aus welcher Vorhersagen auf Basis von Beobachtungen aus der Vergangenheit mittels einer Übergangsmatrix hergeleitet werden.
Das klassische Beispiel hierzu ist die Prognose des Wetters. Wir definieren vereinfacht drei Zustände: sonnig ("sunny"), bewölkt ("cloudy") und anderes (Regen, Schnee - "other"). Aus den Beobachtungen der Vergangenheit wissen wir, dass in 17% der Fälle die Sonne scheint, wenn am Vortag die Sonne geschienen hat (wenn ich 100 Tage "sunny" beobachte, wird an 17 Folgetagen auch die Sonne geschienen haben). Ebenfalls ist beobachtet worden, dass es am Folgetag zu 20% bewölkt war und in 63% der Fälle das Wetter von Typ "other" eingetroffen ist. In Summe muss somit am nächsten Tag einer der drei Zustände eingetroffen sein. Die gleichen Überlegungen können auch auf den Zustand "cloudy" und "other" angestellt werden. Es sind somit die jeweiligen Zustände zu identifizieren und das darauf folgende Wetter am nächsten Tag abzuzählen, woraus sich die Übergangsmatrix ergibt, welche folgend anhand unserer Beobachtungen zusammengestellt ist.
Wenn wir nun die Wahrscheinlichkeit eines bewölkten Tages für morgen bestimmen wollen, gegeben dass es heute sonnig ist, dann ist einfach der entsprechende Zellenwert (hier 20%) zu nehmen. Wie sieht es aber nach zwei Tagen aus? Oder anders: Wie hoch ist die Wahrscheinlichkeit, dass es in zwei Tagen bewölkt ist, gegeben dass es heute sonnig ist? Hierzu sind alle verschiedenen Kombinationen von heute an zu addieren.
Wir beginnen mit dem Pfad "sunny -> sunny -> cloudy". Die Wahrscheinlichkeit hierfür beträgt 17% * 20% = 3.4%
Ein weiterer möglicher Pfad lautet "sunny -> cloudy -> cloudy": 20% * 58% = 11.6%
Der letzte mögliche Pfad lautet "sunny -> other -> cloudy": 63% * 45% = 28.35%
(Die Leseart am Beispiel "sunny -> sunny -> cloudy" ist wie folgt: heute ist es sonnig, morgen (Tag 1) ist es sonnig und übermorgen (Tag 2) ist es bewölkt.).
Die Summe der möglichen Pfade ergibt dann die gesuchte Wahrscheinlichkeit: 3.4% + 11.6% + 28.35% = 43.35%.
Prinzipiell lässt sich der hier dargestellte Markow Prozess über eine Matrixmultiplikation in Excel realisieren, was aber schnell mühsam wird. Mit Excel und MC FLO ist dies mit der Formel fmc_SimpleMarkovChain hingegen kinderleicht.
Aber es sind nicht allein die Endzustände von Relevanz, sondern andere Faktoren, welche ebenfalls stochastisch sind, also von Unsicherheit geprägt sind. Und somit kommen wir zum zweiten Beispiel.
Stellen wir uns vor, dass wir ein Hospital betreiben, welches verschiedene Kategorien der Kostenallokation definiert hat: Heimbetreuung, Stationär, Intensivmedizin, und Todesfall. Aus der Vergangenheit liegt folgende Übergangsmatrix vor, welche für die zukünftige Planung herangezogen werden soll:
So sehen wir, dass ein Patient in Heimbetreuung mit 95% Wahrscheinlichkeit auch am nächsten Tag eine Heimbetreuung in Anspruch nehmen wird und in 3% der Fälle einer stationären Behandlung bedarf. Die Wahrscheinlichkeit am nächsten Tag Intensivmedizin in Anspruch zu nehmen oder gar zu versterben beträgt in Summe 2%.
Für die Heimbetreuung (alternativ kann auch von "geheilt" die Rede sein) fallen für das Krankenhaus keine Kosten an. Für die übrigen Kategorien liegen Daten aus der Vergangenheit vor, welche als Wahrscheinlichkeitsfunktion im folgenden Excel (ab Zelle F10) abgelegt sind (die Zahlen sind rein fiktiv). Anhand der Übergangsmatrix möchten wir die Kosten der nächsten drei Tage inklusive heute bestimmen (Tage 0 bis 3), gegeben dass eine bestimmte Anzahl Patienten zurzeit betreut wird (Zelle E9ff., neue Patienten werden aus Vereinfachungsgründen erst am 4. Tag aufgenommen).
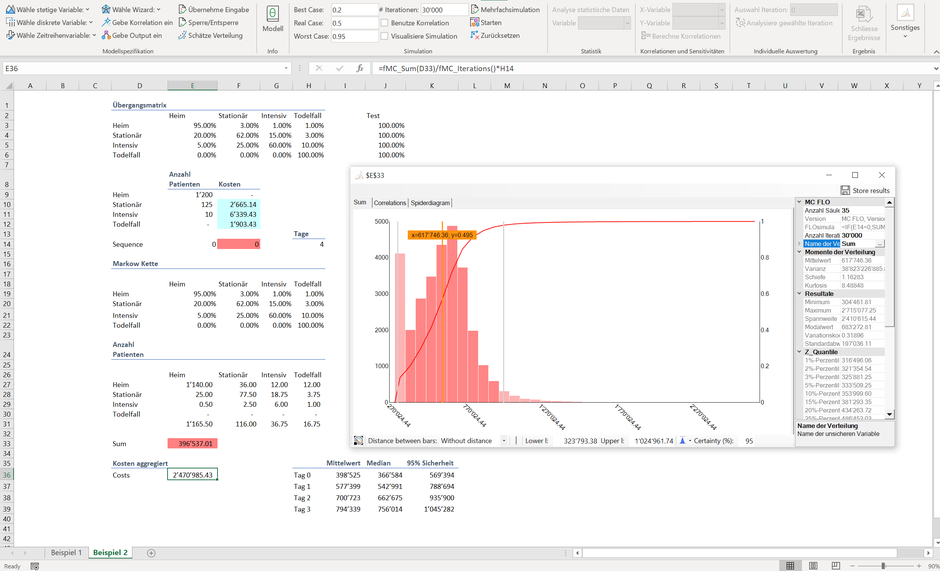
Nach Simulation und unter Rückgriff der Übergangsmatrix betragen die Kosten im Mittel ca. 2.5 MCHF für heute und die nächsten drei Tage (Zelle E36), die durchschnittlichen Kosten der Tage 0 bis 3 sind in Spalte I ab Zeile 36 dargestellt. Aufgrund der Streuung der Kosten sind Durchschnittswerte jedoch nicht sinnvoll, da die Kosten mehrheitlich vom Betreuungspersonal abhängig sind und die Kapazitätsplanung des Personals über den Grad der Sicherheit gesteuert wird. Wir möchten nun neu erfahren, wie hoch die Kosten jeweils sind, gegeben dass diese mit angenommener 95%-Sicherheit einen gesuchten Schwellenwert nicht überschreiten. Und da die Kapazitätsplanung tagesscharf erfolgen soll, ist die Sicherheit von 95% jeden Tag anzusetzen (der 95% Sicherheitsgrad kann wie folgt interpretiert werden: wir sind uns zu 95% sicher, dass die geplanten Mittel ausreichen werden).
Mit MC FLO können wir über die Funktion fmc_FinancialValue die gesuchte Grösse für die einzelnen Tage kinderleicht ermitteln. Die Lösung ist in Spalte K abgetragen.
So sehen wir, dass das 95% Perzentil weitaus höhere Kosten als der "Durchschnitt" ausweist (für den Tag 3 liegt dieser mit 1 MCHF deutlich über den Mittelwert von 0.8 MCHF). Eine Kapazitätsplanung, welche hingegen nur auf den Durchschnitt ausgerichtet ist, liegt nur knapp über den Median (50% Perzentil, Spalte J). Oder mit anderen Worten: wer mit Durchschnittswerten eine Kapazitätsplanung aufsetzt, darf sich über den mangelnden Personalbestand der eingeteilten Schichten nicht beklagen. Besser ist beraten, wer die Personalplanung daher mittels einer Simulation unter Berücksichtigung des Grad der Sicherheit aufsetzt.
Mit Markow-Ketten und einer Simulation können Sie bessere Vorhersagen treffen.
Epilog: Markow-Ketten können auch bei der Unternehmensplanung und der damit verbundenen Prognose sinnvoll eingesetzt werden. Als konkreter Anwendungsfall sind die Finanzierungskosten eines Unternehmens zu nennen. Sollen beispielweise Anleihen in den nächsten Jahre ausgegeben werden, kann die Zinslast in Abhängigkeit der Rating-Einstufung über einen Markow-Prozess simuliert werden.
(P.S.: Uns ist bewusst, dass bei teuren Operationen das Material und nicht das Personal für die hohen Kosten verantwortlich ist; der geneigte Leser möge uns dies verzeihen. Zudem ist es so, dass die Planung der Kapazitäten im Voraus vorzunehmen ist; gedanklich kann der Tag 0 daher in die Zukunft projiziert werden).




Kommentar schreiben