Auch wenn wir das oben erwähnte Phänomen bereits in mehreren Blogs (etwa hier) beschrieben und demaskiert haben, kommen uns immer wieder Beispiele unter, in der das grundlegende Prinzip des zentralen Grenzwertsatzes nicht umgesetzt ist.
Wie bekannt bemühen wir uns mit einem Beispiel um Klärung. Stellen wir uns vor, dass wir 10 Produkte einer Reparatur unterzogen und die Kosten bereits vorliegen haben. Bevor die Produkte ausgeliefert werden, sind diese einer Qualitätskontrolle zu unterziehen, was mit weiteren Kosten verbunden ist. Aus der Vergangenheit wissen wir, dass die Kosten der Qualitätskontrolle proportional zu den Reparaturkosten sind und diese gleichverteilt zwischen 10% und 90% der Reparaturkosten schwanken. Die Qualitätskontrolle benötigt jedoch Zeit und das Management möchte bereits die Planung unter Berücksichtigung der Gesamtkosten aufsetzen. Dabei möchte es im Plan einen Betrag einstellen, von dem auszugehen ist, dass die Gesamtkosten den eingestellten Betrag nur noch mit einer "Wahrscheinlichkeit" von 10% übertreffen können. Welcher Betrag sollte in der Planung einfliessen?
Nun, wir beginnen mit dem falschen Ansatz: Der Multiplikation der sicheren Kosten aus der Reparatur mit einer unsicheren Variablen in Bezug auf die Qualitätskontrolle.

In diesem Fall wird unterstellt, dass der Aufschlag für die Qualitätskontrolle gleichzeitig und für alle Produkte zwischen 10% und 90% schwanken kann. Das 90% Sicherheitsniveau liegt dann bei ca. 350'000 CHF. Sie gehen in diesem Fall somit davon aus, dass in 90% der Fälle die Gesamtkosten zwischen dem Minimum von 202'000 und 350'000 CHF zu liegen kommen. Um das obigen Modell vor Augen zu führen: In Iteration 1 der Simulation wählt der Zufallsgenerator einen Aufschlag von sagen wir 70% aus, was zur Folge hat, dass Produkt 1, Produkt 2, mithin alle Produkte jeweils mit 70% angesetzt werden. Die Wahrscheinlichkeit, dass alle Produkte zur gleichen Zeit den gleichen Zuschlagssatz annehmen, ist aber bereits bei 10 Produkten verschwindend gering. Die Arbeiten für die Qualitätskontrolle sind daher in unserem Fall unabhängig von den einzelnen Produkten anzusetzen, womit für jedes Produkt ein unterschiedlicher Aufschlag für die Qualitätskontrolle zugeordnet werden muss.
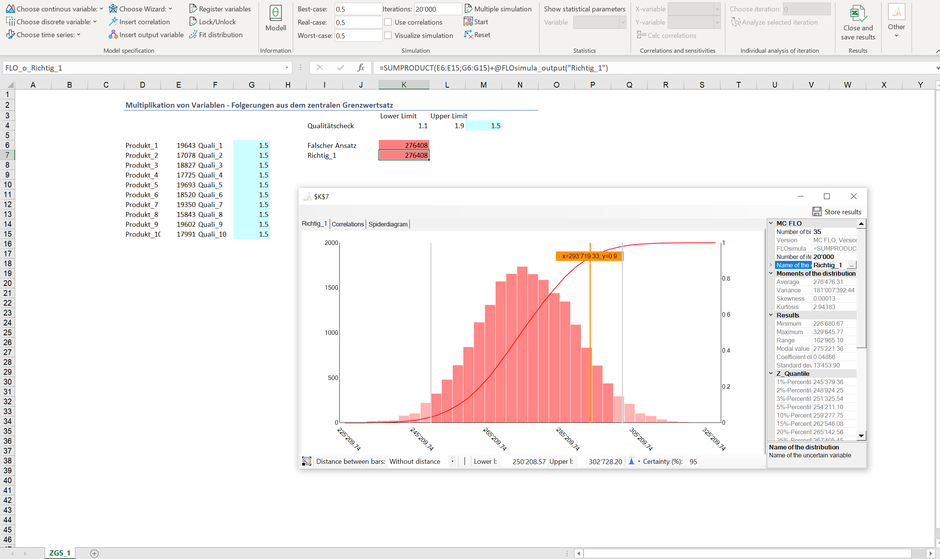
Wir haben das entsprechende Modell nun so erweitert, dass für jedes einzelne Produkt eine individuelle Verteilung in Bezug auf die Qualitätskontrolle zugeordnet ist. Anbei das Ergebnis nach einer Simulation mit 20'000 Iterationen
Bei der korrekten Berechnung ("Richtig_1") zeigt sich, dass das 90% Sicherheitsniveau bei ca. 293'000 CHF liegt, also erheblich tiefer als die vormals berechneten 350'000 CHF. Das eingangs als Gleichverteilung wahrgenommene Ergebnis entpuppt sich bei der korrekten Umsetzung als normalverteilt. Dies ergibt sich direkt aus dem zentralen Grenzwertsatz, wonach die Summe von n unabhängigen Verteilungen mit endlicher Varianz approximativ normalverteilt ist.
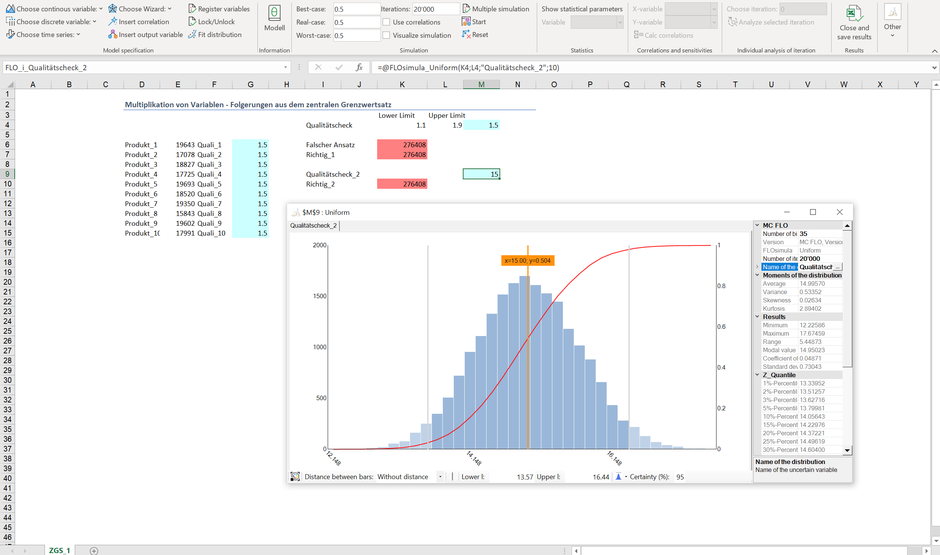
Nun, wenn Sie nun 20 oder mehr Produkte haben, dann ist das Zusammentragen von weiteren Verteilungsfunktionen relativ aufwendig und ehrlich gesagt, nicht notwendig. Mit MC FLO können Sie alternativ jeder Verteilungsfunktion die Anzahl Vorkommnisse als zusätzlichen Parameter nach dem Variablennamen mitgegeben (der Vorgang wird als Faltung oder "Convolution" bezeichnet).
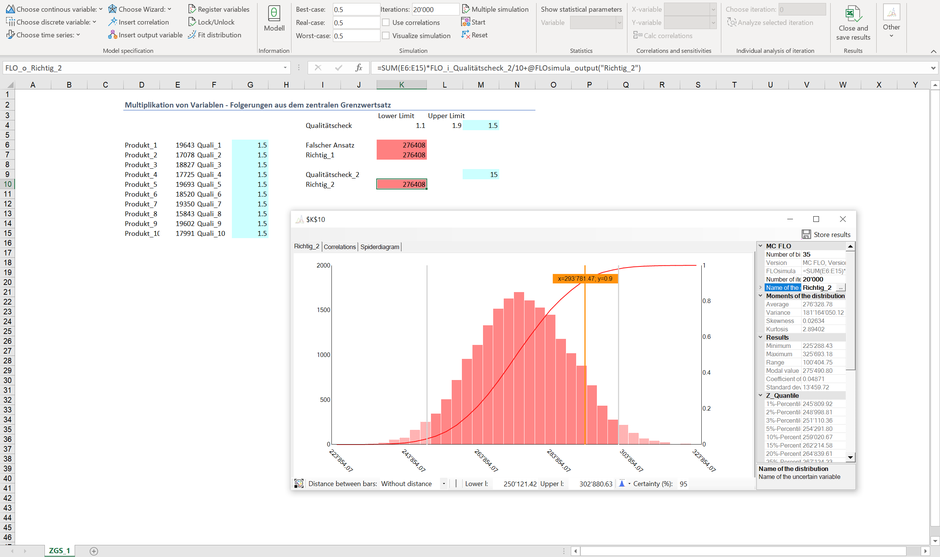
Wenn Sie 10 Vorkommnisse mit einem Erwartungswert von 1.5 CHF je Produkt summieren, resultiert die obige Verteilung, dies bei einem Erwartungswert von 15 CHF. Um die Gesamtkosten zu ermitteln, ist als letzter Schritt eine entsprechende Outputvariable zu definieren und das Ergebnis der Faltung zu normieren. Das Resultat sehen Sie sie folgend:
Auch hier liegt das 90% Sicherheitsniveau bei knapp 293'000 CHF. Für die Bestimmung der Produktkosten wäre im letzten beschriebenen Ansatz ("Richtig_2") sogar nur eine Inputvariable notwendig.
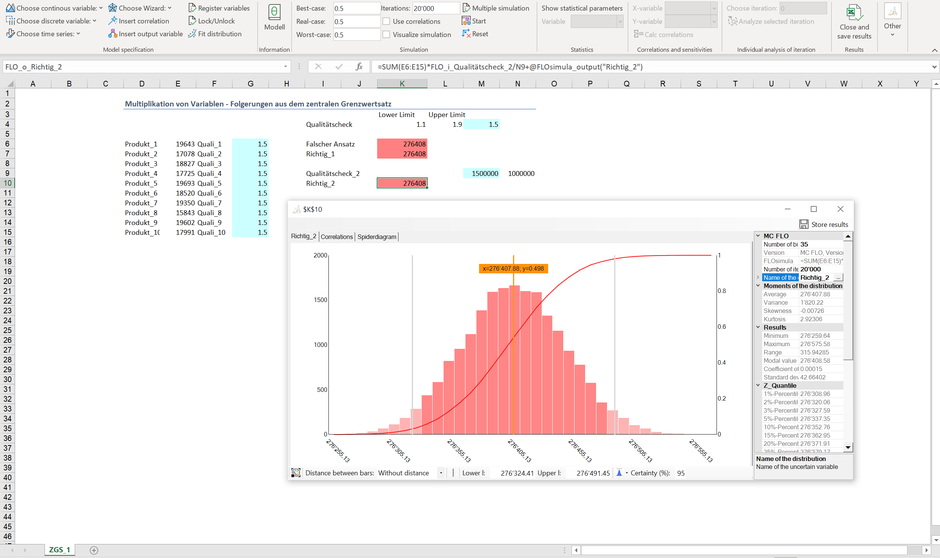
Nun, bevor wir uns auf unsere Lorbeeren ausruhen, eine Klarstellung: Wenn Sie tausende Produkte nach diesem Ansatz für einen gleichwertigen Sachverhalt berechnen wollen, verzichten Sie auf eine Simulation. Das 90%-Sicherheitsniveau nähert sich mit Anzahl Vorkommnisse immer mehr und mehr den Erwartungswert an.
Anbei das Ergebnis mit 1'000'000 Produkten - die Abweichung vom Erwartungswert ist geradezu vernachlässigbar: die Werte auf der x-Achse streuen ja kaum.
Um eine aktuelle Frage nachzugehen: Wenn die Kosten einer Impfung pro Person gleichverteilt zwischen 20 Euro (bester Fall, Minimum) und 40 Euro (schlechtester Fall, Maximum) betragen, wie hoch werden die Impfkosten für 10 Mio. Menschen im besten und im schlechtesten Fall sein? Genau: In beiden Fällen werden die Gesamtkosten sehr nah beim Erwartungswert von 300 Mio. Euro liegen.
P.S.: Das Prinzip der Faltung ist fester Bestandteil jeder Verteilungsfunktion in MC FLO. So können Sie Auswirkungen (etwa Schadensausmass) und Anzahl Fälle, beides als unsichere Variablen vorliegend, kombinieren.
P.S.2: Der zentrale Grenzwertsatz kann nicht dafür herhalten, auf eine Simulation zu verzichten. In der Praxis sind nur selten die Voraussetzungen gegeben, um allein auf Mittelwerte abzustützen.

Kommentar schreiben