In den letzten Blogs haben wir die Monte-Carlo Simulation im Kontext einer Vielzahl von praktischen Entscheidungsproblemen vorgestellt, insbesondere im Bereich der Unternehmensplanung. Wir beleuchten hier weitere Einsatzgebiete von Simulationen und dabei zwei einfache, in der Praxis aber häufige Probleme anreissen.
Wir beginnen mit der Integration, in der Mathematik und im Ingenieurwesen unausweichliche Instrumente zur Bestimmung von Flächen unter einer Kurve oder Abwandlungen davon. Wer die höhere Schule besucht hat, wird hierzu Begriffe wie die Stammfunktion verinnerlicht haben. Sind jedoch komplizierte Kurven zu analysieren, ist der Weg über eine Stammfunktion - wenn überhaupt vorhanden - ein steiniger. Oftmals sind Approximationen oder eben eine Monte-Carlo Simulation der bessere Weg.
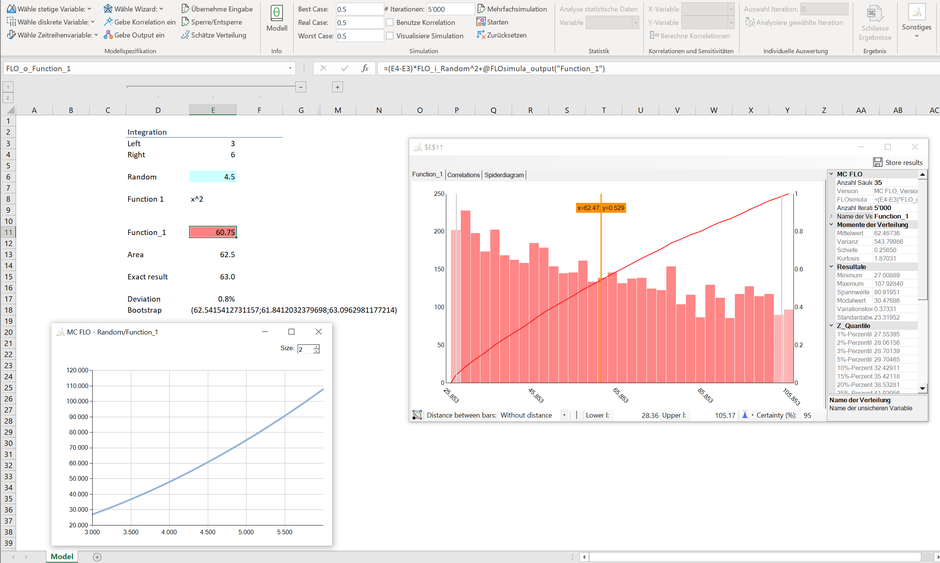
Stellen wir uns vor, dass wir die Fläche der durch f(x) = x^2 vorgegebenen Kurve im Intervall zwischen 3 und 6 ermitteln möchten. Die Stammfunktion lautet 1/3x^3, die Fläche ergibt sich schulbuchmässig aus 1/3*6^3 - 1/3*3^3 = 63. Anstatt auf Stammfunktionen zurückzugreifen, können wir die Fläche durch direkten Rückgriff auf die Funktion und einer Simulation bestimmen.
Wie aus Zelle E13 ersichtlich, beträgt der mittlere Flächeninhalt der Simulation bei 5'000 Iterationen 62.5, was eine Abweichung von 0.8% vom exakten Wert darstellt (das mittels Bootstrap ermittelte Konfidenzintervall [95%] liegt bei [61,8, 63,1]).
Gewiss, das vorgetragene Beispiel ist aufgrund der einfachen Stammfunktion ohne Simulation rasch lösbar. Versuchen Sie aber folgende Funktion f(x) = exp((4x^2+12x^3)/(3x-12x^2)) im gleichen Intervall zu integrieren. Eben, besser ist doch wohl die Simulation.
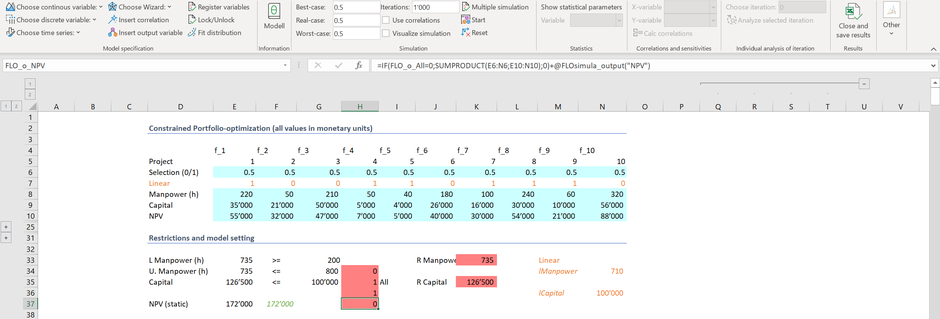
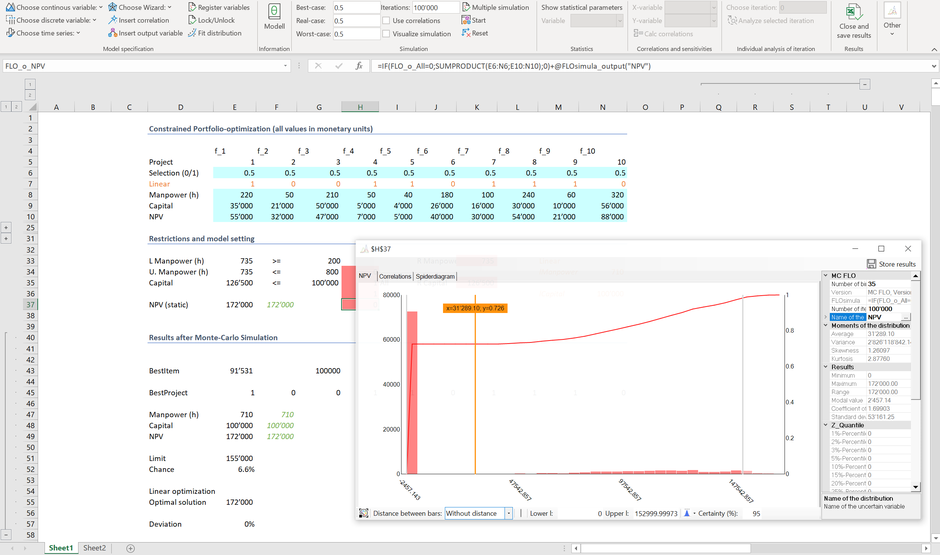
Das zweite Beispiel dürfte ebenfalls vielen Schülern:innen und Studenten:innen bekannt sein: die lineare Optimierung. Folgend sind 10 Projekte aufgeführt, mit entsprechendem Arbeitseinsatz ("Manpower"), Investitionen ("Capital") und Barwerten ("NPV") je Projekt. Welche Projekte sollen umgesetzt werden, gegeben, dass die Investitionen und der Arbeitseinsatz gewisse Bedingungen (Zeile 33 & 35) einhalten?
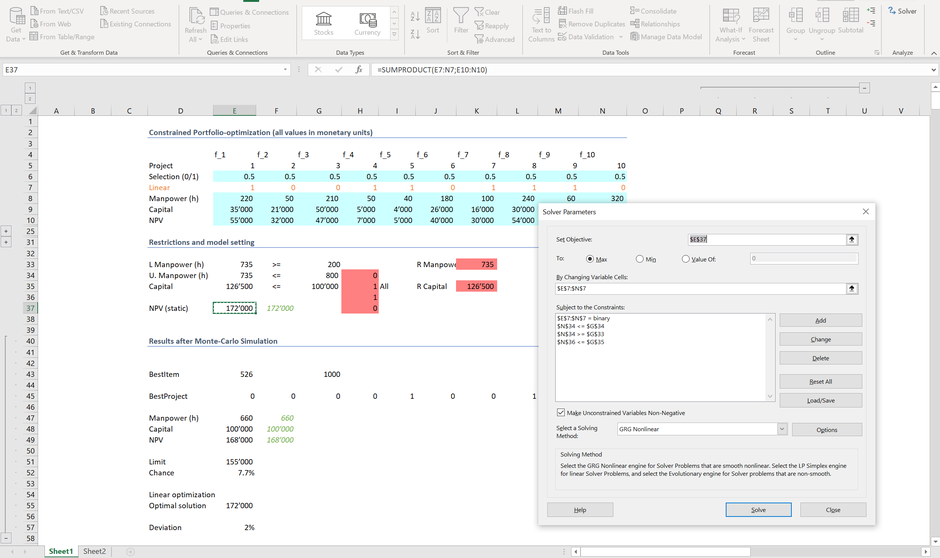
Das gängigste Verfahren zur Lösung ist der Simplex-Algorithmus, der in unserem Fall auch eine optimale Lösung liefert; hierzu haben den wir den in Excel verfügbaren "Solver" herangezogen, welcher einen maximalen NPV von 172'000 CHF ermittelt. Die Selektion der Projekte erfolgt in Zeile 7 (das Projekt 1 [Zelle E7] wird ausgewählt, das Projekt 2 [Zelle F7] hingegen nicht).
Statt auf den Simplex Algorithmus abzustützen, können wir alternativ auf die Monte-Carlo Simulation zurückgreifen. Hierzu haben wir in Zeile 6 für jedes Projekt Bernoulli Variablen definiert, welche den Wert 0 (nicht ins Portfolio aufnehmen) oder 1 (ins Portfolio aufnehmen) mit jeweils 50% Wahrscheinlichkeit annehmen können. Mit nur 500 Iterationen wird das optimale Ergebnis nur knapp verfehlt; die Abweichung liegt gerade bei 4% (Zelle E57).
Während die gängigen Optimierungsverfahren wie der Simplex-Algorithmus rasch exakte Lösungen liefern können, da sie auf deterministische Ausgangsbedingungen aufsetzen, besticht die Monte-Carlo Simulation durch den Ausweis von Wahrscheinlichkeiten. Das ist der Kern. Denn im täglichen Kontext erleben wir es immer wieder, dass "optimale" Bedingungen nicht den Alltag bestimmen, so dass die Zielgrösse verschwimmt
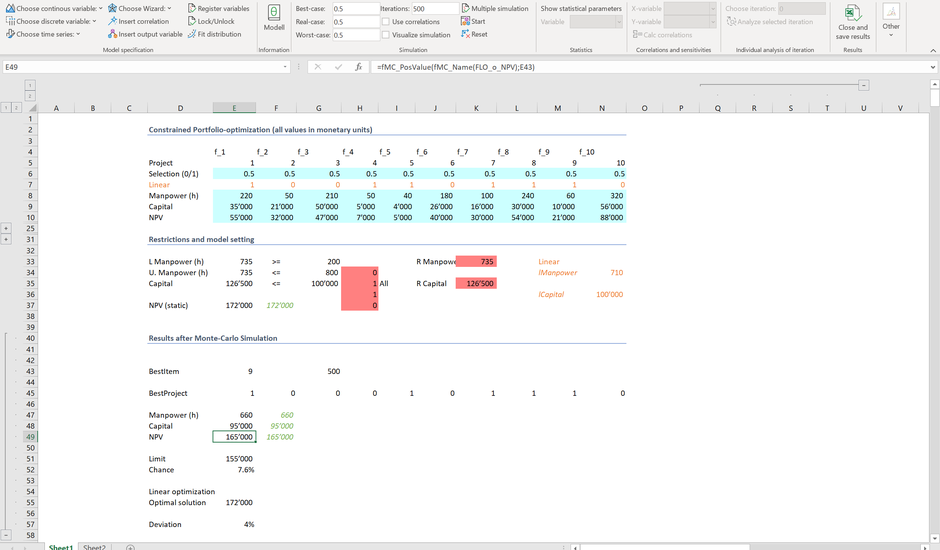
Wir starten nun neu eine Simulation mit 10'000 Iterationen. Das Resultat nach einigen Sekunden zeigt einen maximalen NPV von 172'000 CHF. Die Wahrscheinlichkeit ein Ergebnis von über 155'000 CHF zu erzielen, gegeben, dass alle Nebenbedingungen eingehalten werden, beträgt aber nur ca. 6.6%*.
Fazit: Es ist wie mit dem Gang in den Wald. Wenn Sie vorhaben einen Baum zu fällen, nehmen Sie eine Axt mit. Für alle anderen Fälle dürfte ein Taschenmesser sinnvoller sein.
*Es ist nicht von ungefähr, dass viele Kennzahlen im öffentlichen Verkehr in der DACH Region während des Lockdowns im Frühjahr 2020 zwar Bestwerte erreichten, aber das "Optimum" trotz idealer Voraussetzungen verfehlten. Es gibt immer eine Variable, welche ausschert. Analog ist dies auf andere Performancemasse übertragbar: durch den Beizug von deterministischen Instrumenten wird angenommen, dass die Unsicherheit ausgeblendet und somit eliminiert werden kann. Eine Simulation zeigt hingegen effektiv auf, ob eine Ambition realistisch ist.

Kommentar schreiben