Kennen Sie die Szene aus den Film "Avengers: Infinity War", in welcher Dr. Strange 14'000'605 mögliche Ausgänge aus dem Kampf gegen den Titan Thanos vor dem geistigen Auge sah und nur in einem Fall die Avengers diesen zu ihrem Gunsten entscheiden konnten? Wie lässt sich damit erklären, dass die Avengers - durch die Hand von Iron Man (aka Tony Stark) - am Schluss doch noch den Sieg errungen konnten? Nun, Hollywood wäre nicht Hollywood, wenn solche Wunder nicht geschehen würden. Aber auch die Statistik - insbesondere die Bayessche Auffassung - führt uns zur Antwort, womit die Wahl von Dr. Strange - den entscheidenden Zeitstein dem Titan Thanos auszuhändigen - objektiv begründet wird.
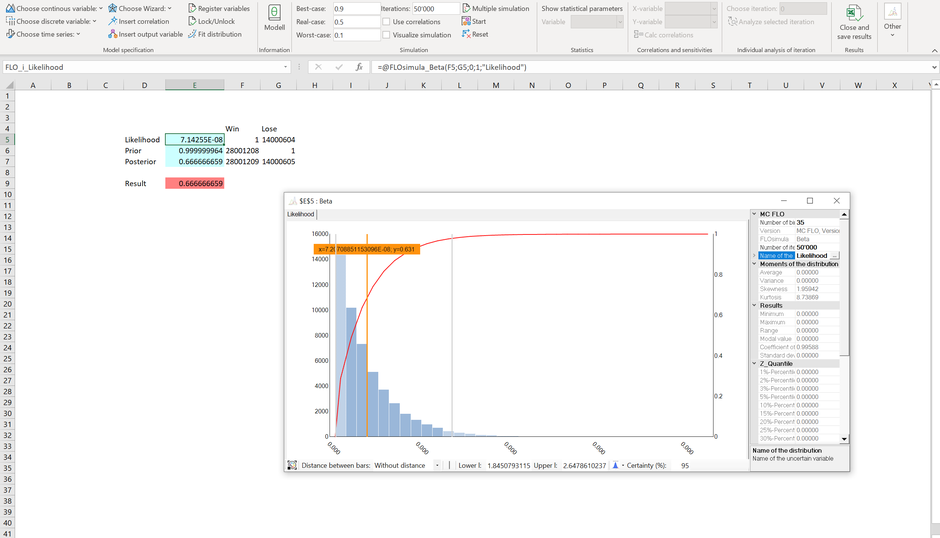
Fangen wir mit den "Fakten" an: Dr. Strange kann nur in einem von den möglichen 14'000'605 Fällen einen positiven Ausgang zugunsten der Avengers erkennen. Die Erfolgswahrscheinlichkeit beträgt somit 1 zu 14'000'604. Diese "Messung" können wir als Wahrscheinlichkeitsverteilung - im Konkreten über eine Betaverteilung - darstellen ("Likelihood").
Allein unter Rückgriff der Daten müssen wir festhalten, dass es ein Ding der Unmöglichkeit darstellt, Thanos zu besiegen.
In der Bayesschen Statistik wird auf eine Ursprungswahrscheinlichkeit oder a-priori Wahrscheinlichkeit zurückgegriffen, welches aufgrund eines allgemeinen Vorwissens gewonnen wird. Bis zur Folge "Avengers: Infinity War" haben sowohl die Zuschauer als auch Dr. Strange beobachten können, wie die einzelnen Teammitglieder oder als Ganzes verschiedene unmögliche Situationen haben meistern können. Die Kraft und insbesondere die Genialität eines Tony Stark scheinen dabei keine Grenzen zu kennen. Auch dieses Vorwissen kann als Wahrscheinlichkeitsverteilung aufgefasst werden. Nehmen wir an, dass die Avengers als so gut befunden werden, dass sie in 28'001'208:1 Fällen scheinbar unmögliche Situationen für sich entscheiden können. Die Avengers sind somit verdammt gut, aber auch sie können verlieren (es sei schon hier gesagt: wenn wir als a-priori Wahrscheinlichkeit davon ausgingen würden, dass die Avengers zu 100% alle Situation meistern werden, dann würde das Beziehen von Daten - auch wenn diese das Gegenteil beweisen würden - die a priori Wahrscheinlichkeit nicht dominieren können. Daher hier der allgemeine Rat, nie von 100% Sicherheit auszugehen).
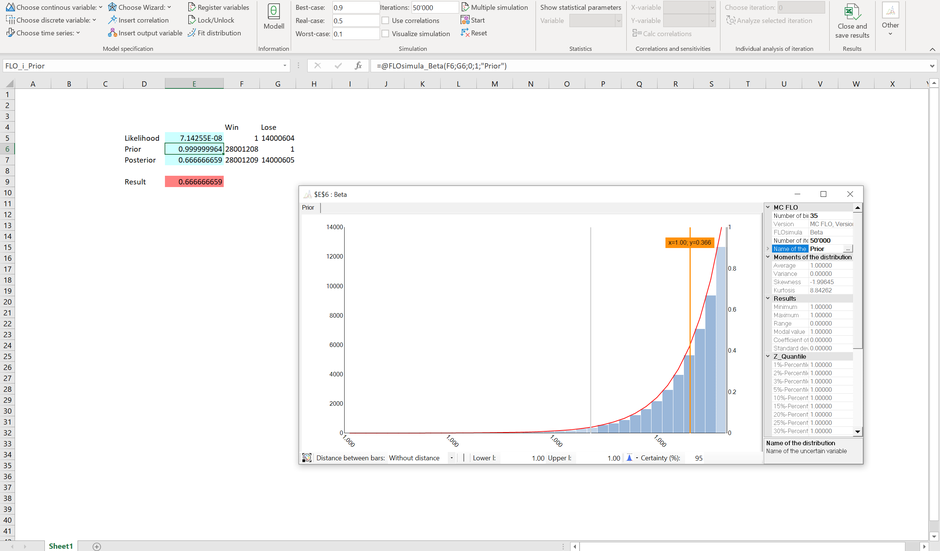
Folgend die a-priori Wahrscheinlichkeitsverteilung ("Prior"):
Im Gegensatz zu oben ist die Wahrscheinlichkeit zu verlieren extrem gering. Oder mit anderen Worten: Mit der Beta Verteilung bei einem alpha Parameter von 28'001'208 und beta Parameter von 1 wird von einem Grad der Sicherheit von knapp 100% zugunsten der Avengers ausgegangen.
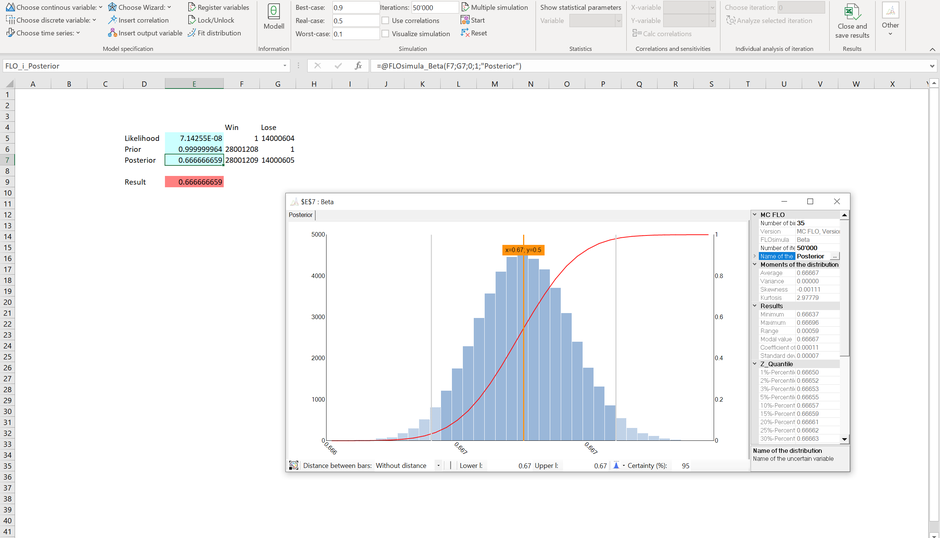
Der Kern der modernen von Bayes geprägten Statistik ist das Zusammenführen des Vorwissens mit den Daten, woraus wieder neues Vorwissen generiert wird. Liegen beide Verteilungen als Beta Verteilung (zwischen dem Intervall [0,1]) vor, kann die gesuchte Posterior Verteilung durch Addition der Treffer ("Win") und Nicht-Treffer ("Lose") als angepasste Beta Verteilung dargestellt werden (wenn die Posterior Verteilung von der gleichen Klasse wie das Vorwissen ist, dann können beide Verteilungen kombiniert werden; "conjugate prior"):
Durch Kombination beider Verteilungen resultiert nun ein Grad der glaubwürdigen Erwartung von knapp 67%, das die Avengers im Kampf gegen Thanos am Schluss doch noch den Sieg erringen können. Für den Zuschauer sollte es daher spannend bleiben.
Das Original entstammt dem Kapitel Han Solo and Bayesian Priors aus "Bayesian Statistics the fun Way: Understanding Statistics and Probability with Star Wars, LEGO, and Rubber Ducks" von Will Kurt.

Kommentar schreiben