Es gibt im täglichen und im wissenschaftlichen Kontext kaum ein Begriff, dass so oft Stirnrunzeln bei den befragten Personen auslöst wie das des Risikos. Uns verwundert dies nicht, denn wir halten getreu dem Statistiker Sam Savage* die Aussage aufrecht, dass Risiko immer im Auge des Betrachters liegt.
Sehr oft wird Risiko als etwas zukünftig Negatives, Schädliches, Vermeidvolles interpretiert. Andere Auffassungen legen hingegen nahe, dass Risiken als Schwankungen um den Erwartungswert einer Zielvorgabe anhand von Gefahren und Chancen beschrieben werden sollten. Die gängigen Organisationen und deren Standards (etwa ISO 31000), welche sich Risiken auf die Fahne geschrieben haben, vertreten zunehmend Letzteres. Beide Auffassungen sind sich einig, dass das Risiko zukunftsbezogen ist.
Als Ökonomen können wir den unterschiedlichen Begriffsdefinitionen nicht viel abgewinnen; für uns geht es um Entscheidungen unter Unsicherheit (auf Englisch «uncertainty»; die deutsche Sprache kennt sogar den Begriff der «Ungewissheit», was sogar eine Nuancierung bedingt, aber das lassen wir mal so stehen). Kernelement bei Entscheidungen unter Unsicherheit ist, dass die meisten uns bekannten und vorliegenden Daten/Handlungsalternativen nicht genau oder exakt vorliegen, eine Entscheidung aber trotzdem getroffen werden muss.
Als Entscheidungsinstanz würden wir immer gerne wissen, welche Menge unsere Kunden im nächsten Quartal nachfragen, welche Innovationen unsere Mitbewerber in der Pipeline haben, etc. Alles dies kennen wir nicht und es würde uns einfach zu viel kosten, die relevanten Informationen zu besorgen, bevor eine Entscheidung getroffen wird (diese Ausführungen haben mit der Pandemie und der globalen Erderwärmung wieder an Bedeutung gewonnen: lohnt es sich zu warten, bis genügend Daten für die Entscheidungsfindung vorliegen oder ist es dann eventuell zu spät?).
In Ermangelung solcher Daten ist ein Rückgriff auf Annahmen, welchen den «Grad der glaubwürdigen Erwartung» widerspiegeln nicht nur geboten, sondern gar erforderlich. Die Bayessche Auffassung der Statistik lehrt uns, dass alle unsicheren Parameter (Treiber) als Wahrscheinlichkeitsverteilung aufzufassen sind, womit eine Planung, welche sich nur auf einen Wert fokussiert, eben keine Bedeutung hat**.
So, nun aber wieder zum praktischen Beispiel:
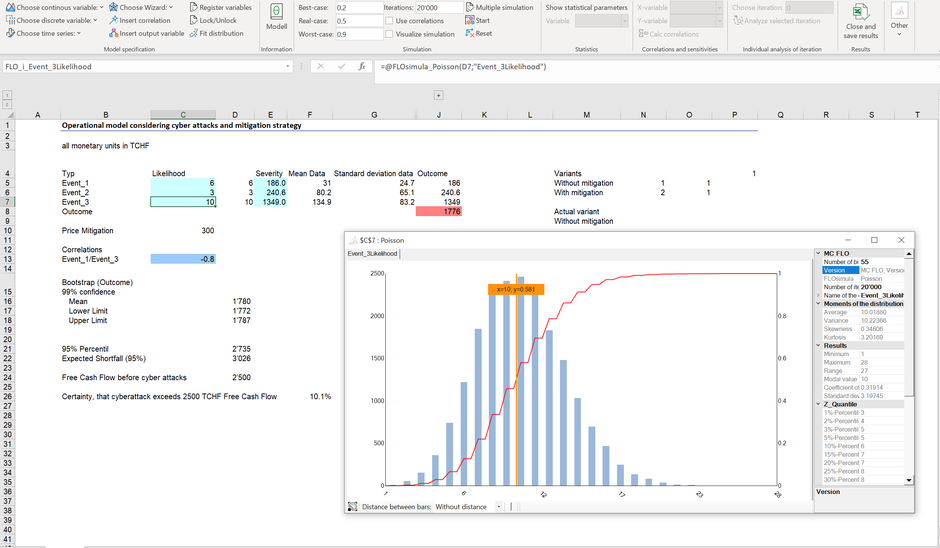
Folgend sind drei Fälle potentieller Schäden durch Cyberangriffe (Event_1…Event_3) aufgeführt, wobei die Anzahl Fälle pro Jahr (Spalte C2:C5) als Poisson Verteilung und der potentielle Schadensausmass je Fall als Log-Normalverteilung Verteilung (E2:G5) dargestellt sind.

In allen drei Fällen gilt es als betroffenes Unternehmen festzuhalten, dass es sich um schädliche Risiken aufgrund der negativen Auswirkung eines Cyberangriffes handelt, unabhängig davon, ob der Schaden klein, gross oder im Erwartungswert zu liegen kommt. Aus Sicht des Angreifers handelt es sich womöglich jedoch ausnahmslos um Chancen (von der Möglichkeit einer strafrechtlichen Verfolgung abgesehen), um die eigene Reputation zu erhöhen. Anhand dieses Beispiels sollte klar sein, dass das Risiko nicht einfach zu umschreiben und somit immer im Kontext des Betrachters aufzufassen ist.
Im weiteren Verlauf adaptieren wir aber den Begriff der möglichen Abweichungen um einen Planwert als Risiko, so wie dieser im Standard ISO 31000 verankert ist. Dies führt unweigerlich zu Frage, was als Planwert zu definieren ist. Die gängige Auffassung geht davon aus, dass der Planwert «erwartungstreu» zu sein hat, was auf den Mittelwert aller möglicher Realisierungen hinausläuft. Für die Fälle Event_1 bis Event_3 ist der erwartete Schadenausmass in den Zellen J2:J5 abgetragen. Was sagt diese Grösse im Einzelnen und aggregiert genau aus? Für Event_1 beträgt bei einer angenommen mittleren Anzahl von 6 Fällen pro Jahr und bei einem erwarteten Schaden von im Mittel 31 TCHF pro Fall, dass im Erwartungswert von einem jährlichen Schaden von 186 TCHF auszugehen ist. Setzen wir zudem voraus, dass die möglichen Fälle und die Auswirkungen auf das Schadensausmass unabhängig voneinander sind (eine höhere Anzahl von Schadensfällen von Event_1 pro Jahr hat keinen Einfluss auf die möglichen Auswirkungen des Schadens), dann entspricht der erwartete Schaden aller drei Fälle in Höhe von 1’776 TCHF genau der Summe der Erwartungswerte der einzelnen Schäden. Diese Erkenntnis folgt automatisch aus dem «Zentralen Grenzwertsatz der Statistik», wonach die Summe von n unabhängigen Variablen (mit endlicher Varianz) gegen eine Normalverteilung konvergiert. Das aggregierte erwartete Risiko entspricht in diesem Fall (und nur in diesem Fall) genau der Summe der einzelnen Risiken, oder anders: 1+1=2. Folgend sei dies an unserem Beispiel dargestellt.

Wie ersichtlich und mit der bootstrap Technik (Zellen C15ff.) anhand einer Monte-Carlo Simulation untermauert, kann der wahre Erwartungswert durch das ermittelte Konfidenzintervall entsprechend approximiert werden. Aus der Graphik ist zudem ersichtlich, dass der Erwartungswert mit fast 50% Wahrscheinlichkeit übertroffen wird.
Zwei Probleme knüpfen an diese Darstellung an: a) kaum ein Unternehmen kann und sollte sich an Erwartungswerte orientieren oder planen Sie das Kostenbudget eines Jahres so, dass (symmetrische Verteilung der Variablen vorausgesetzt), im Mittel mit einer Budgetüberschreitung alle 2 Jahre zu rechnen ist? Eben. Und b), das Konzept einer linearen Aggregierung fällt mit der realistischen Annahme, dass die Variablen nicht unabhängig sind. Jedes Unternehmen kennt es: Werden die Preise gesenkt oder erhöht, dann reagieren die Kunden darauf sehr unterschiedlich, was eine Abhängigkeit zwischen den Variablen untermauert.
Oder anders: Falls Sie nicht allein an Mittelwerten interessiert und / oder Abhängigkeiten zu berücksichtigen sind, dann sind Monte-Carlo Simulationen nicht nur geboten, sondern gar erforderlich, um eine datenbasierte Entscheidung herbeizuführen. So, und da sind wir nun bei den Entscheidungen.
Alle die bisher dargestellten Ausführungen sind ohne Wert, wenn sie nicht mit einer Referenz verglichen werden. Die erste und einfachste Überlegung lautet: Ist das Unternehmen in der Lage die möglichen Bedrohungen finanziell zu stemmen? Falls wir davon ausgehen, dass der Free Cash Flow vor Cyberangriffe bei 2’500 TCHF lag und erst bei einem negativen Free Cash Flow von einem Konkurs auszugehen ist, dann würde der Rückgriff auf den oben ermittelten erwarteten Schaden zu einer Entwarnung führen. Aber nur relativ, da die Wahrscheinlichkeit einen höheren Schaden als den Erwartungswert hinzunehmen, bei - wie bereits dargestellt - approximativ 50% liegt. Rein statistisch wäre das Unternehmen somit im Mittel nach 3 Jahren Konkurs. Interessanter ist jedoch der Wert, der mit einer gewissen Wahrscheinlichkeit nicht überschritten wird und uns Auskunft darüber geben kann, welche Massnahmen zu treffen sind.
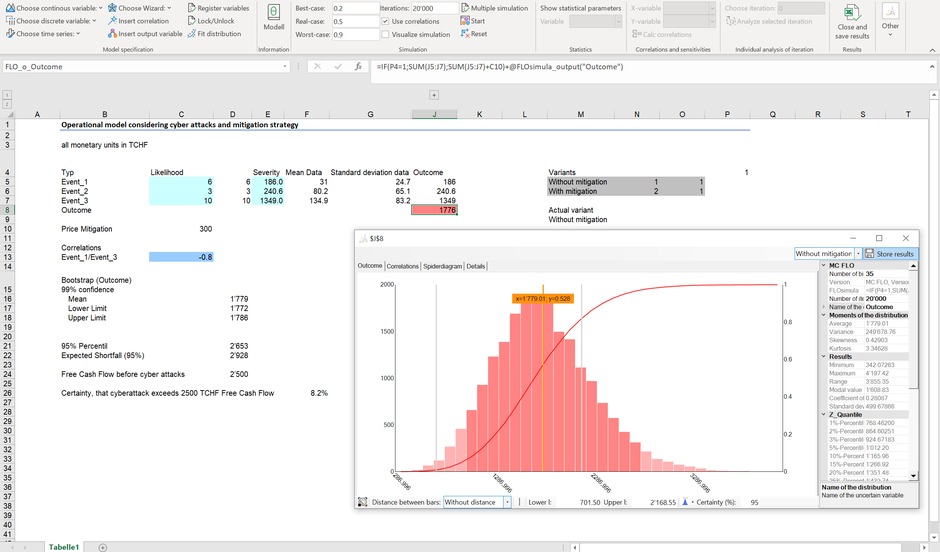
Gehen wir davon aus, dass das Unternehmen die grössten Schäden von 5% nicht decken möchte. Neu sei zudem angenommen, dass ein Unternehmen einen Cyberschutz anbietet, welches die Anzahl der schädlichen Angriffe für Event_1 und Event_3 um die Hälfte reduziert. Der Preis eines solchen Schutzes beträgt 300 TCHF pro Jahr. Aus der Vergangenheit liegen zudem Zahlen vor, welche auf eine hohe negative Korrelation zwischen den Ereignissen 1 und 3 schliessen lässt.

Unter Ausblendung des Cyberschutzes und mit Einbezug der Korrelation beträgt der Schaden bei einem Sicherheitsniveau von 95% (100% - 5% nicht tragfähiger Schaden) bei ca. 2'650 TCHF, mit dem Cyberschutz liegt der Schaden bei gleichem Sicherheitsniveau hingegen bei ca. 1'990 TCHF.
Bei einem Free Cash Flow von 2'500 TCHF ist somit der Bezug eines Cyberschutzes die effizientere Möglichkeit den Konkurs des Unternehmens abzuwenden, auch wenn im «Mittel» und ohne Beizug der Abhängigkeiten ein jährlicher Schaden von nur 1'776 TCHF resultiert. Die Strategie des Bezugs der Cybersicherheit wird klarer, wenn wir uns den durchschnittlichen Verlust anschauen, welcher bei Durchbrechung der nicht tragfähigen Verluste von 5% auftritt (Expected shortfall). Auch hier liegt der Wert von ca. 2'220 TCHF unter dem Free Cash Flow von 2'500 TCHF. Eine absolute Garantie ist dies aber nicht, da das Maximum des Cyberschadens bei über 3'000 TCHF zu liegen kommt. Immerhin, ein Cyberschaden von über 2'500 TCHF wird nur in 0.5% der Fälle erwartet.
Zusammengefasst: Wenn Sie von einem Grad der glaubwürdigen Erwartung gemäss Spezifikation ausgehen können, dann lautet die Entscheidungsregel unter Unsicherheit in diesem Fall den Cyberschutz in Anspruch zu nehmen (aber Achtung: die Hacker werden ihren Zug antizipieren können und neue Möglichkeiten ausprobieren).
P.S: In der Excel Datei finden Sie das Vorgehen, wie die Daten einer Log-Normalverteilung in die Exponentialnotation – wie sie MC FLO verwendet – transformieren können. Zudem sei nochmals darauf hingewiesen, dass die Multiplikation von mehreren pro Jahr anfallenden Ereignissen nicht unbesehen mit dem Schadensausmass multipliziert werden darf; stattdessen ist auf das Konzept der Faltung («Convolution») zurückzugreifen.
*Sam Savage: The Flaw of Averages: Why We Underestimate Risk in the Face of Uncertainty, 2012.
** 02.06.2021: Wir finden, dass alle mögliche Ereignisse mit einer Wahrscheinlichkeitsverteilung beschrieben werden können; im einfachsten Fall kann zudem die Laplace-Regel (Annahme der Gleichverteilung) zu einer Quantifizierung beitragen.

Kommentar schreiben