Um es vorweg zu nehmen: Wir sind keine Freunde der Risikomatrix, müssen aber zugeben, dass diese in vielen Bereichen weiterhin genutzt wird.
So wie das Layout der Tastaturanordnung einer Schreibmaschine zum Ziel hatte, den Fluss des Schreibens möglichst wenig zu brechen, ist es Aufgabe der Risikomatrix die Darstellung der Gefahren innert kürzester Zeit zu vereinfachen. Dabei ist zu berücksichtigen, dass in der Anfangszeit der Risikomatrix die Technik der Monte-Carlo Simulation noch zu wenig verbreitet war, respektive noch viel Zeit in Anspruch nahm, um alle «Risiken» aggregiert und unter Berücksichtigung von Abhängigkeiten («Korrelationen») entscheidungsrelevant aufzubereiten. Die weiterhin weite Verbreitung der Risikomatrix ist gemäss Ökonomen auf Pfadabhängigkeiten zurückzuführen: Die Menschen sind es einfach gewohnt, Risiken über eine Matrix abzubilden.
Kritiken zur Risikomatrix sind reichlich vorhanden (siehe auch unser Blogbeitrag), aber die alternative quantitative Darstellung über ein Tornado Graph (welche auf eine Korrelationsanalyse aufsetzt) braucht eine Umgewöhnung.
Für diejenigen Personen, die eine quantitative Analyse schätzen, die Resultate davon aber in einer Risikomatrix abzubilden haben, stehen in MC FLO nun die geeigneten Instrumente bereit.
Ziel einer umfassenden quantitativen Analyse mittels Monte-Carlo Simulation ist eine objektiv begründbare Entscheidungsempfehlung unter Berücksichtigung von Unsicherheit, etwa bei den Absatzmengen oder Anzahl Cyberangriffe, welches ein Unternehmen ausgesetzt ist.
Im Kontext der klassischen Unternehmensplanung ist als primäres Ziel die Erwirtschaftung eines ökonomischen Gewinns zu nennen, welche für einige Unternehmensgesellschaften sich approximativ als Summe der Cash Flow's von operativer (unter Einschluss der Zinslast für Fremdkapital) und Investitionstätigkeit herleiten lässt. Als Mindestziel ist ein ökonomischer Gewinn von 0 anzustreben; dieser stellt sicher, dass alle Forderungen von Seiten Lieferanten, Arbeitnehmer und Fremdkapitalgeber soweit bedient werden können, dass noch genügend Luft für notwendige Investitionen in Sach – und immaterielle Anlagen verbleibt. Der Zweck der Unternehmensplanung liegt sodann im Aufzeigen geeigneter Massnahmen, um das primäre Ziel zu erreichen. Dabei sind insbesondere die Treiber zu identifizieren, welche das gesuchte Ziel massgeblich – sowohl in positiver als auch negativer Sicht – beeinflussen.
Eine «integrierte» Unternehmensplanung hat zum Zweck, das heutige Wissen in die Zukunft zu projizieren und Massnahmen abzuleiten, um den Unternehmensfortbestand zu sichern. Da die Zukunft nicht mit Sicherheit vorherbestimmt werden kann, sind alle relevanten Treiber als Bandbreite über eine Wahrscheinlichkeitsverteilung anzugeben. Integriert bedeutet aber auch, dass nicht nur die Erfolgsrechnung mit der Bilanz und der Cash-Flow Rechnung (inklusive den vorgelagerten Teilplänen, etwa die Personalplanung) miteinander verwebt sein müssen, sondern dass alle Faktoren, welche auf den Unternehmenserfolg einzahlen, einheitlich bemessen sein müssen. Aus unserer Sicht ist nur eine quantitative Analyse hierzu in der Lage, zumal das Management sehr oft mit den gleichen Fragen konfrontiert ist: «Was wird passieren, wenn die Absatzmenge um x% einbricht? Wie sicher können wir sein, dass der Gewinn positiv ist?» etc. Dabei vertreten wir einen Ansatz, in der «Wissen» als Daten aufbereitet in die Entscheidungsfindung einfliesst. Somit kann die qualitative Analyse in eine quantitative überführt werden. Die Zielgrösse wird somit als Bandbreite über eine Wahrscheinlichkeitsabschätzung beschrieben («wie hoch ist die Wahrscheinlichkeit [oder auch Grad der Erwartung], dass der Free Cash Flow im Planungszeitraum in Summe mindestens 0 CHF beträgt?»).
Es sind sodann von der strategischen bis zur operativen Ebene diejenigen Treiber zu identifizieren, welche das spezifische Geschäftsmodell bestimmen, um dann im Rahmen einer Monte-Carlo Simulation wahrscheinlichkeitsorientierte Aussagen zur Zielgrösse treffen zu können.
Schauen wir das mit MC FLO mitgelieferte Basisbeispiel ("MC FLO Test.xlsx") näher an*. Neben den Absatzmengen zum Produkt sind Annahmen zu Preisen, Wachstum, Kosten und einem «Störfaktor» zu treffen.
Die klassische Planung nimmt oftmals eine Trennung der Treiber vor: Die Kosten und Umsätze werden quantifiziert und in die Planungswerkzeuge übernommen; eher a priori qualitative Artefakte wie potentielle Störfaktoren bestenfalls als Szenario, schlimmstenfalls als Bestandteil einer Risikoanalyse mittels Risikomatrix überführt und somit einer integrierten quantitativen Analyse entzogen. Noch schlimmer – weil ineffizient - wird es, wenn die Treiber sowohl in der Unternehmensplanung als auch in der Risikoanalyse Eingang finden.
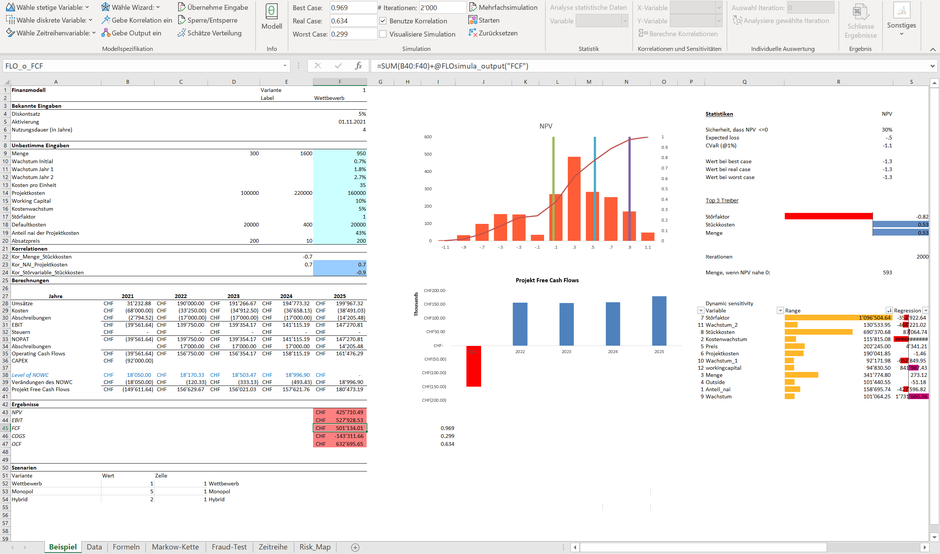
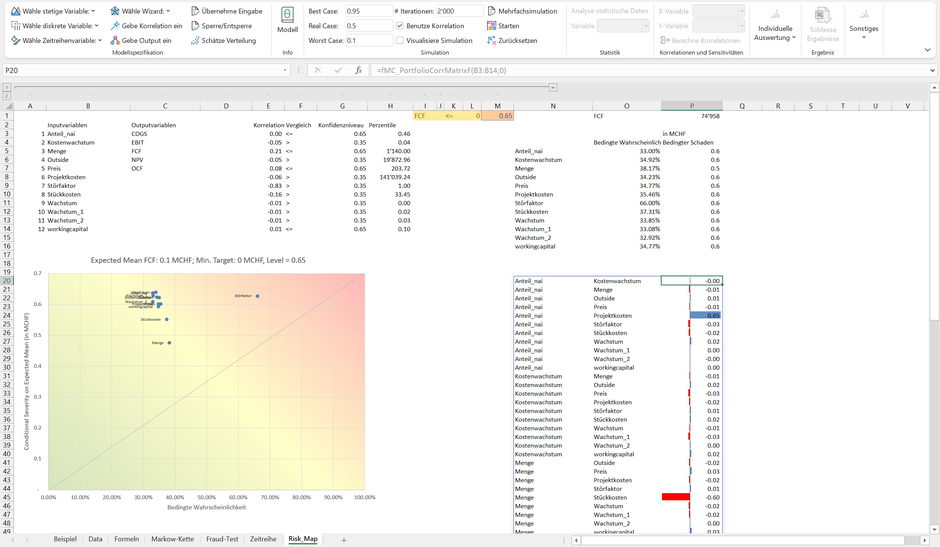
Die automatische Herleitung der Risikomatrix aus der Unternehmensplanung, wobei diese als Zielgrösse ein Free Cash Flow (FCF) von CHF 0 über die Planungsperiode vorgibt, ist folgend dargestellt.
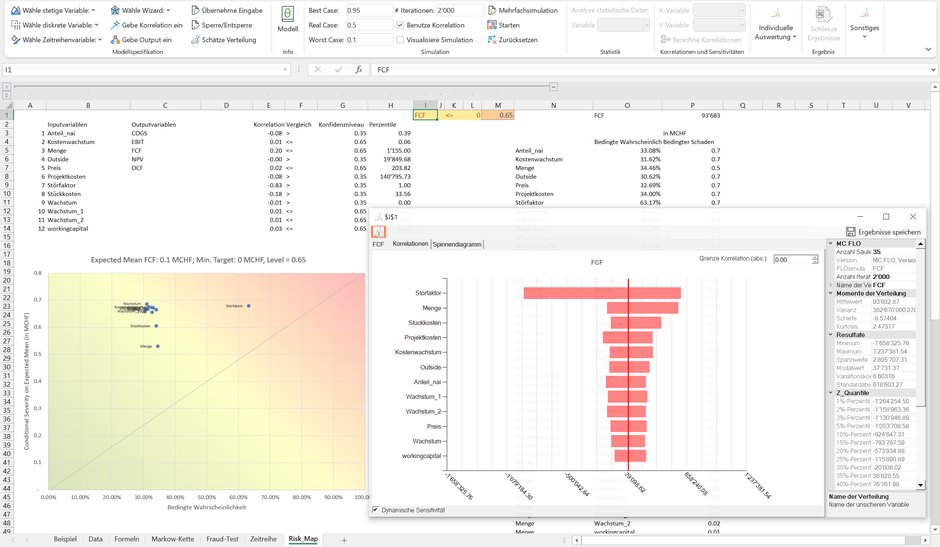
Die Werte der Risikomatrix links unten haben wir in Spalte O und P - abgeleitet aus der in Zellen I1:K1 definierten Zielgrösse- abgetragen. So beträgt die Wahrscheinlichkeit, dass der FCF unter CHF 0 fällt, gegeben dass die Menge den Wert bei P65 (Spalte G; P65 = 65% Perzentil) von 1'115 Einheiten nicht überschreitet (Spalte H; d.h.: P65 also 65% der Ergebnisse zu den Mengen liegen unterhalb der Schwelle von 1'115**), ca. 34.36% (Spalte O)***. Der durchschnittliche Schaden bei einer Unterschreitung des FCF von CHF 0, gegeben, dass die Menge tiefer als 1'115 Einheiten ausfällt. liegt dabei bei MCHF 0.5 (Spalte P). Gefährlich sind somit Kombinationen, bei denen die bedingte Wahrscheinlichkeit als auch der bedingte Schaden gross sind, etwa beim «Störfaktor». Entsprechend wird diese Variable in der bedingten Risikomatrix im roten Bereich dargestellt. Das Äquivalent in der dynamischen Sensitivität**** ist die Einordnung der Variablen «Störfaktor» als oberster Eintrag. Ersichtlich ist, dass eine Veränderung des Störfaktors einen deutlichen Einfluss auf den Erwartungswert des FCF ausübt. Der nächste Eintrag in der dynamischen Sensitivitätsanalyse ist die Variable «Menge», gefolgt von den «Stückkosten» (bei 2'000 Iterationen). Wie ersichtlich entfaltet «Menge» im linken Bereich (links vom vertikalen Balken, welcher den Erwartungswert des FCF abbildet) eine geringere Kraft als im rechten Bereich. Insgesamt ist die Auswirkung aber auch hier gering, was zur Einordung im gelben Bereich der Risikomatrix führt.
Aus Managementsicht bedeutet eine rote Einstufung, dass die dort abgebildeten Variablen einen hohen Einfluss auf die Zielgrösse ausüben und daher prioritär gesteuert werden müssen. In unserem Fall trifft dies bei der Variable «Störfaktor» zu.
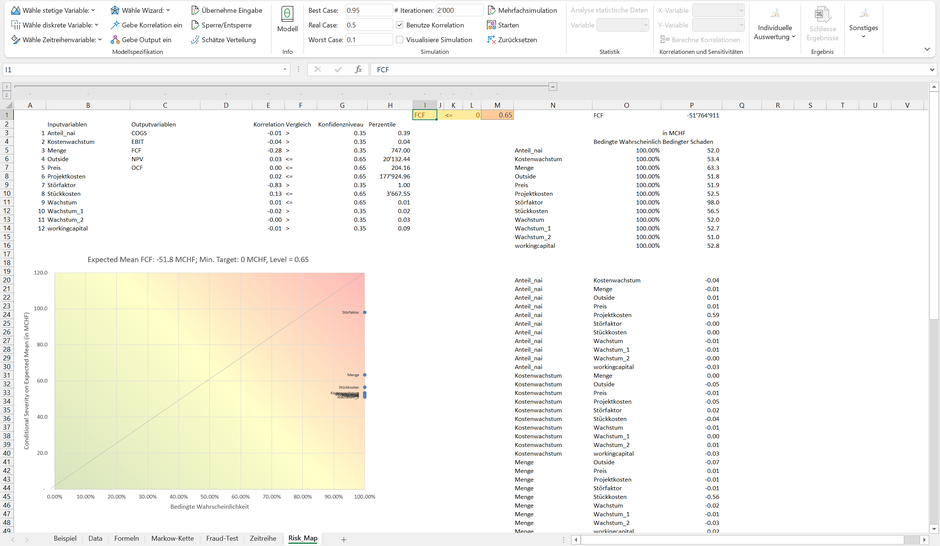
Obwohl die bedingte Risikomatrix mehrheitlich konsistent mit der dynamischen Sensitivitätsanalyse ist, sind einige potentielle Stolpersteine zu berücksichtigen. Passen wir das Modell nun so an, dass die Stückkosten zwischen CHF 3’000 und CHF 4’000 variieren können und somit die Wahrscheinlichkeit, einen FCF von kleiner CHF 0 zu erwirtschaften, 100% beträgt (d.h.: egal welche Variation für die Variable innerhalb der Modellspezifikation vorgenommen wird, die Wahrscheinlichkeit den FCF über CHF 0 zu hieven, beträgt 0%).
In diesem Fall befinden sich alle Variablen auf der rechten Vertikalen der bedingten Risikomatrix, und auch hier wird die Variable «Störfaktor» als einflussreichste Variable identifiziert. An einer Weiterführung des Unternehmens ist bei dieser Modellkonstellation aber nicht zu denken. In diesem Fall ist die Unternehmensaufgabe geboten.
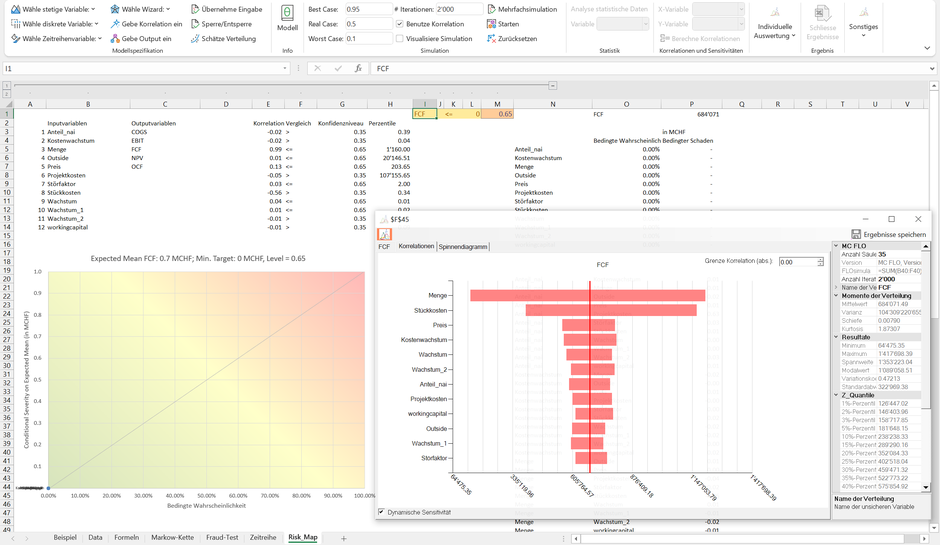
Etwas anders sieht der Fall aus, wenn die Wahrscheinlichkeit einen FCF kleiner CHF 0 zu erwirtschaften bei 0% liegt. Hierzu lassen wir die Stückkosten im Vergleich zum Ausgangsmodell zwischen CHF 0.3 und CHF 0.4 variieren und limitieren den Höchstwert der Projektkosten auf CHF 120'000. Nun liegen in der bedingten Risikomatrix alle Variablen auf dem Koordinatenursprung; da eine Anpassung der einzelnen Variablen nicht zu einem FCF kleiner CHF 0 führt, sind die entsprechenden Wahrscheinlichkeiten ebenfalls 0, womit die Konzentration auf den einen Punkt (im grünen Bereich) erklärt werden kann. Sie können sich somit auf die faule Haut legen und den Zufall walten lassen. In keinem Fall werden Sie – wohlgemerkt innerhalb der Modellspezifikation – einen FCF kleiner CHF 0 vergegenwärtigen müssen.
Die dynamische Sensitivitätsanalyse zeigt hingegen unabhängig von der Zielgrösse auf, welche Variablen den stärksten Einfluss auf den FCF ausüben – dies auf Basis des Erwartungswertes (welcher hier positiv ist).
Ein letzter Stolperstein ist aus dem Weg zu räumen: Die bedingte Risikomatrix spannt das Resultat einer dynamischen Sensitivitätsanalyse in die Dimension Eintrittswahrscheinlichkeit und Schadensausmass auf; eine Multiplikation dieser Variablen zur Umkehrung ist jedoch nicht möglich, da die Basis jeweils eine unterschiedliche ist. Auch hier wieder der Rückgriff auf das Beispiel. Bei der Bemessung der Eintrittswahrscheinlichkeit liegt folgende Frage zu Grunde: «Wie wahrscheinlich ist es, dass der FCF kleiner 0 ist, gegeben, dass die Menge kleiner als 1'115 zu liegen kommt?». Die Bedingung ist somit an die Menge geknüpft. Bei der Kalkulation des Schadensausmasses ist die Frage hingegen folgende: «Wie hoch wird der Verlust beim FCF sein, gegeben, dass die Menge kleiner 1'115 und der FCF kleiner als 0 ist». Die Bedingung ist somit an die Menge und einem vorab definierten FCF Niveau geknüpft.
Prolog: Ein Nachteil der Risikomatrix ist, dass es Abhängigkeiten zwischen den einzelnen Variablen nicht betont. Mit der in MC FLO eingebauten Funktion fmc_PortfolioCorrMatrixF können alle Korrelationen mit den jeweiligen Korrelationskoeffizienten (Pearson oder Spearman) ausgegeben und somit die Abhängigkeiten sichtbar gemacht werden.
Falls die «Störvariable» mit anderen Variablen hoch korrelieren sollte, dann folgt daraus, dass in erster Instanz die Ursache identifiziert und im Anschluss der ursächliche Treiber als erstes gesteuert werden sollte.
Fazit: Die bedingte Risikomatrix kann anhand von bedingten Eintrittswahrscheinlichkeiten und bedingten Ausmass die Notwendigkeit einer aktiven Intervention zur Erreichung der Ziele einer Planung herangezogen werden, wobei die bekannte visuelle Darstellung beibehalten wird.
*Das Standardbeispiel besteht nur aus einer vereinfachten Cash-Flow Rechnung; ein Beispiel zur integrierten Unternehmensplanung können Bezüger einer nicht zeitlich beschränkten Lizenz mittels E-Mail an support@mcflosim.ch anfordern (siehe auch diesen Blogbeitrag).
**ob P65 oder (1-P65) genommen wird, hängt vom Vorzeichen des Korrelationskoeffizienten mit der untersuchten Variablen - hier FCF - ab. Die Menge ist positiv mit dem FCF korreliert. Das P65 Niveau "scheidet" die 35% höchsten Mengen aus der Mengenverteilung aus (das entspricht dem rechten Rand der Verteilungsfunktion). Die Stückkosten sind hingegen negativ mit dem FCF korreliert. Das P65 Niveau scheidet in diesem Fall die 35% tiefsten Stückosten aus der Stückkostenverteilung aus (das entspricht dem linken Rand der Verteilungsfunktion). Die Auswahl des Px Wertes - auch als Ambitionslevel bezeichnet - ist unternehmensabhängig zu treffen. Selbstverständlich kann für jede Variable ein unterschiedlicher Ambitionslevel vorgegeben werden. Eine analoge Interpretation kann über den "Value-at-risk" Ansatz vorgenommen werden.
***Alle anderen Input - oder Eingangsvariablen fliessen modellkonsistent - unter Berücksichtigung von Korrelationen zur untersuchenden Variablen - in die Berechnung ein.
****Als Standardwerkzeug zur Analyse, welche Treiber das gesuchte Ergebnis massgeblich beeinflussen, ist der Beizug einer dynamischen Sensitivitätsrechnung im Rahmen einer Monte-Carlo Simulation Standard. Sie beantwortet anhand einer Perzentilbetrachtung die Frage, welcher Wert im besten und im schlechtesten Fall zu erwarten ist.
Update 03.08.2021: Fehlerkorrektur Ambitionslevel, erweiterte Fussnoten.

Kommentar schreiben