Wussten Sie, dass MC FLOsim und das Monte-Carlo Simulations Add-In MC FLO seinen Ursprung zum oben genannten Thema hat?
Für die Interessierten hier die Kurzform: Unternehmen investieren in (Sach – und immaterielle) Anlagen, welche bilanziert und über eine ordentliche Nutzungsdauer abgeschrieben werden. Ist die ökonomische Nutzungsdauer einer Anlage erreicht, ist diese durch eine funktionsäquivalente Anlage zu ersetzen. Während die ordentliche Nutzungsdauer aufgrund von steuerlichen Begebenheiten oder dem Vorsichtsprinzip folgend eher kurz bemessen ist, orientiert sich die ökonomische Nutzungsdauer am trade-off zwischen Beibehalt der vorhandene Anlage (welche im Zeitablauf immer höhere Betriebskosten aufweist) und der Neuinvestition (hoher initialer Geldabfluss bei geringen Betriebskosten und eventuell höheren Einnahmen). Ist zum Zeitpunkt T der diskontierte Wert der Neuinvestition höher als bei Fortführung der bestehenden Anlage, ist die Investition zu tätigen und die alte Anlage aus der Bilanz zu entfernen.
Wie oben angerissen, ist der Zeitpunkt T von viele Faktoren abhängig: die Kosten zum Erhalt der Funktionsfähigkeit der alten Anlage, der Investitionsbedarf der neuen Anlage, die damit verbundenen Kosten des Betriebs und die mit der neue Anlagen inhärente Möglichkeit, neue Einnahmequellen zu generieren oder eine erhöhte Produktivität zu erzielen.
Gehen wir davon aus, dass diese Kenngrössen anhand einer risikobedingten* Modellrechnung (Monte-Carlo Simulation) berechnet wurden und die ökonomische Nutzungsdauer sich als Aufschlag auf die ordentliche Nutzungsdauer ergibt, der Aufschlag einer Exponentialverteilung folgt und deren Parameter aufgrund des Modellsettings für jede Anlage variiert (Spalte G). Durch den Rückgriff auf einer Exponentialverteilung unterstellen wir implizit, dass die Anlagen nicht «altern», also keinem physischen oder organischen Verschleiss unterworfen sind. Dies ist etwa bei Software der Fall.
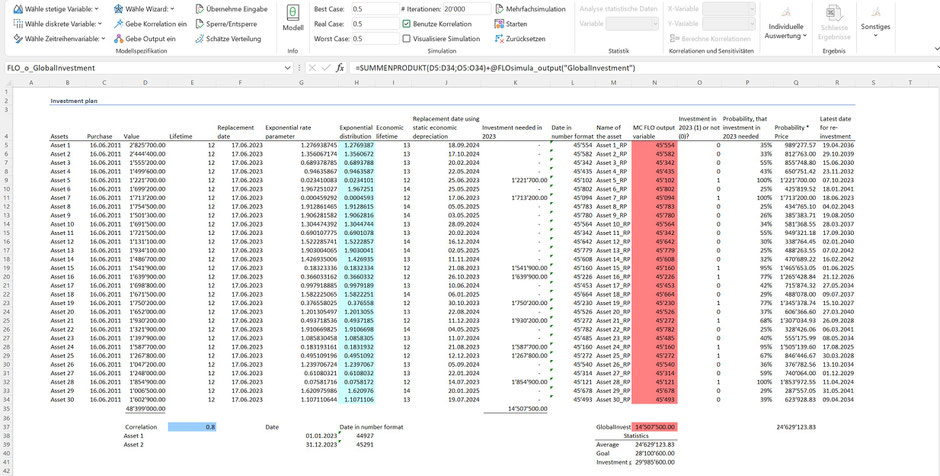
Im folgenden Excel haben wir für unsere 30 Anlagen sowohl den Aktivierungszeitpunkt (Spalte C) die ursprünglichen Anschaffungs- und Herstellkosten (Spalte D) und die ordentliche Nutzungsdauer von 12 Jahren (Spalte E) hinterlegt. Wir unterstellen, dass alle Anlagen am 16.06.2011 aktiviert wurden. Nach «Milchbüchlirechnung» unter Zugrundelegung der ordentlichen Nutzungsdauer müssten alle Anlagen am 17.06.2023 (Spalte F) ersetzt sein, was für das Jahr 2023 einen Investitionsaufwand von knapp 48.3 MCHF (Zelle D35, bei angenommenen Wiederbeschaffungspreisen in Höhe der ursprünglichen Anschaffungskosten; ausserdem unterstellen wir, dass die Investitionen zeitlich nicht vorgelagert sind) zur Folge hätte.
Wird hingegen auf die ökonomische Nutzungsdauer abgestützt, ergibt sich – ohne Simulation – ein Erwartungswert von ca. 14.5 MCHF (siehe Zelle K33) für das Jahr 2023. Eine risikobedingte Herleitung unter Anwendung einer Monte-Carlo Simulation und unter Einschluss von Korrelationen zeigt hingegen auf, dass der Erwartungswert bei ca. 24.6 MCHF für das Jahr 2023 zu liegen kommt. Dieser Unterschied lässt sich anhand des zentralen Grenzwertsatzes der Statistik, wonach die Summe von «n» unabhängigen Zufallsvariablen mit endlicher Varianz annähernd normalverteilt ist und der Erwartungswert dieser Normalverteilung annährend der Summe der Erwartungswerte aller n Zufallsvariablen entspricht, erklären. Hierbei gilt es besonders das Wort «annähernd» zu betonen. In unserem Fall ergibt sich doch ein erheblicher Unterschied, was auf den Beizug der Exponentialverteilung, der geringen Anzahl Anlagen («n») sowie der unterstellten Korrelation zwischen Anlage 1 und Anlage 2 zurückgeführt werden kann.
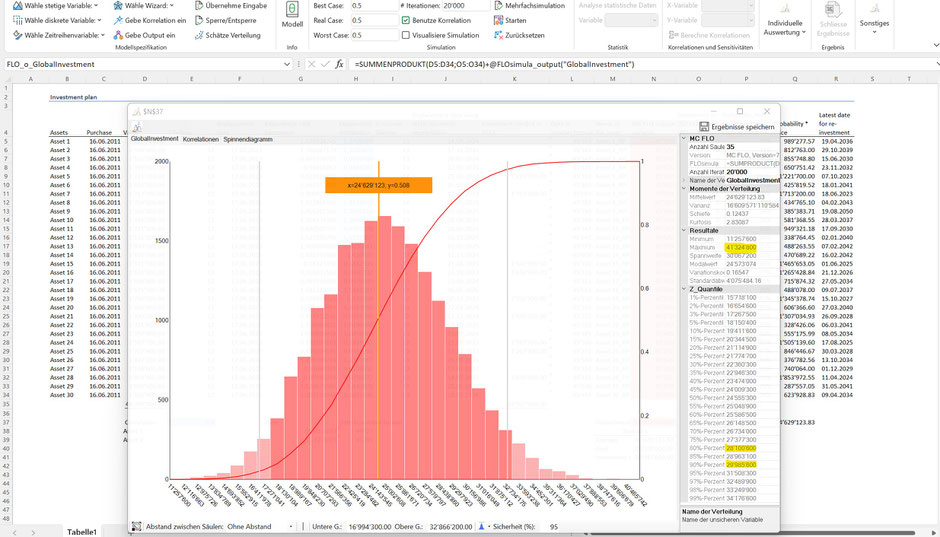
Eine Investitionsplanung oder allgemein eine Geschäftsplanung sollte sich aber nicht allein auf Erwartungswerte abstützen, sondern Ziele vorgeben. Würde in unserem Fall auf den Erwartungswert abgestützt, wäre die Wahrscheinlichkeit einen höheren Investitionsbedarf als die errechneten 24.6 MCHF in Anspruch zu nehmen, bei knapp unter 50%. Kaum ein Manager oder Entscheidungsträger würde darauf eingehen wollen.
Umgekehrt ist die Überlassung aller maximal möglichen Mittel, welche für das Jahr 2023 in Anspruch genommen werden könnten (gemäss Simulation wären dies ca. 41.3 MCHF, siehe Maximum), irrational, da die Wahrscheinlichkeit, dass alle diese Mittel wirklich in Anspruch genommen werden, sehr gering ist und somit unnötig Kapital in der Planung gebunden wäre. Ein realistisches Ziel könnte hingegen lauten, 80% aller für 2023 möglichen Investitionsbedarfe in die Planung einzustellen, in unserem Fall ca. 28.1 MCHF. Sähe das Investitionsreglement eines Unternehmen allgemein vor, dass das Budget für 90% aller möglichen Investitionsbedarfe aufzustellen ist, entspräche das Ziel von 80% einem Anpassungsgrad oder einer Ambition von 10%-Punkten gegenüber dem Ausgangswert (gemäss Investitionsreglement müssten ca. 30 MCHF eingestellt werden; die Ambition von 10%-Punkten führt somit zu einer Anspannung von ca. 2 MCHF).
Natürlich ist uns bewusst, dass die oben skizzierte Herleitung der Modellparameter einer Exponentialverteilung nicht vom Himmel fällt. Die entscheidende Tatsache ist jedoch, dass die Anlagen im Regelfall länger genutzt werden als gemäss Abschreibungsplan vorgesehen und die Investitionsplanung Lösungsmöglichkeiten bieten muss, wie der zukünftige Geldbedarf für Investitionen herzuleiten ist. Hier können anfängliche Erfahrungswerte (welche als «Vorwissen» vorliegen) unter Berücksichtigung einer Gruppierung von Anlagen einen ersten Aufsetzpunkt darstellen. Mit jedem neuen Vorfall, in welcher eine neue Anlage eine alte ersetzt, kann dieses Wissen aktualisiert und entsprechend formalisiert werden.
Fazit: Die stochastische Investitionsplanung formalisiert die Diskrepanz zwischen der ordentlichen und der ökonomischen Nutzungsdauer von Anlagen und schafft unter Beizug einer Monte-Carlo Simulation Transparenz über mögliche und anzustrebende Investitionsplanwerte.
*risikobedingt: hierbei werden Schwankungen um den Erwartungswert explizit berücksichtigt. Die Schwankungen werden dabei mittels Monte-Carlo Simulation modelliert.

Kommentar schreiben