Welche Gemeinsamkeiten haben ChatGPT und der Naive Bayes Klassifikator, so dass sich das Weiterlesen dieses Artikels bereits jetzt schon lohnt?
Im Gegensatz zu klassischen Regressionsmodellen, welche Grenzen im Datenraum ziehen und somit zu den diskriminierenden Modellen gezählt werden, verstehen sich generative Modelle – wie der Naive Bayes Klassifikator und ChatGPT – als solche, welche Daten mittels Verteilungen zusammenfassen und somit in der Lage sind neue Daten zu simulieren.
Basis solcher Modelle ist oftmals (aber nicht nur, ChatGPT ist hierbei eine Ausnahme) die Bayessche Auffassung der Statistik, wonach die Wahrscheinlichkeit, dass Y nach Beobachtung von X zutrifft, aus der Vorabwahrscheinlichkeit (apriori) von Y und der Likelihood ermittelt wird, oder auch P(Y|X) ∝("proportional zu") P(Y) * P(X|Y). P(Y|X) entspricht dabei der Posterior-Wahrscheinlichkeit.
Als Beispiel (siehe Classification_NaiveBayes.xlsx, welches mit MC FLO mitgeliefert wird) haben wir die Daten aus der berühmten Iris („Schwertlilien“) Datenbank zusammengetragen. Anhand der Merkmale Länge und Breite der Kelche („Sepal“) als auch der Blumenblätter („Petal“) ist eine Zuordnung der Datensätze auf die drei Gewächse „Setosa“, „Versicolor“ und „Virginica“ ersichtlich. Während die Längen – und Breitenangaben als numerische Werte vorliegen, sind die Gewächse nicht-numerisch. Insgesamt liegen 120 vollständig klassifizierte Datensätze vor. Im Rahmen eines maschinellen überwachten Lernverfahrens werden die beobachten Daten mindestens in eine Trainings– und in eine Testmenge unterteilt. Anhand des Trainingsmodells werden verschiedene Modelle trainiert. Dasjenige Modell, welches im Rahmen der Testdaten den geringsten „Verlust“ (oder die höchste Übereinstimmung) aufweist, wird dann als Prognosemodell für neue, bisher komplett unbeobachtete Daten herangezogen.
Aus den 120 Datensätzen sind jeweils 40 Datensätze einer der drei Gewächse zugeordnet. Wird davon ausgegangen, dass die Datensätze Resultat einer zufälligen Stichprobe sind, kann als Vorabwahrscheinlichkeit der relative Anteil der jeweiligen Gewächse herangezogen werden (33%, oder 40/120). Auf die Frage hin, ob ein neuer Datensatz „setosa“ zugehörig ist, würde unsere Antwort – ohne Kenntnis der Merkmalausprägungen – somit auf eine Wahrscheinlichkeit von 33% schliessen.
Wie im Blog 2) dargestellt, können wir unter Zuhilfenahme neuer Informationen die Wahrscheinlichkeit schärfen. Gehen wir davon aus, dass wir für einen neuen Datensatz folgende Informationen zu den einzelnen Merkmalen vorliegend haben:
Sepal.Length = 6.3
Sepal.Width = 2.5
Petal.Length=4.9
Petal.Width=1.5
Gegeben die Angaben zu den Merkmalen aus dem neuen Datensatz (etwa «Merkmalausprägung von Sepal.Length beträgt 6.3»), wie wahrscheinlich ist es nun, dass diese Daten dem Gewächs «setosa» entsprechen können, oder dem Gewächs «versicolor» oder «virginica»?.
Der «Naive» Bayes Klassifikator ordnet die Daten eines jeden Merkmals einer Verteilung zu; dabei geht es «naiv» von der Annahme aus, dass die Merkmale «unabhängig» sind und jeweils die gleiche Erklärungskraft bei der Zuordnung auf die einzelnen Gewächse haben. Diese naive Annahme ist in der Realität zwar oftmals nicht gegeben, trotzdem ist die Performance des Klassifikators erstaunlich gut und erlaubt uns die einzelnen Wahrscheinlichkeiten zu multiplizieren.
Für «setosa» sieht es formal wie folgt aus:
P(Y = «setosa»|Sepal.Length=6.3 und Sepal.Width =2.5 und Petal.Length=4.9 und Petal.Width=1.5) ∝ P(Y=“setosa“) *
P(Sepal.Length 6.3|Y=“setosa“)*P(Sepal.Width=2.5|Y=“setosa“)*P(Petal.Length=4.9|Y=“setosa“)*
P(Petal.Width=1.5|Y=“setosa“).
Leseart: Die Wahrscheinlichkeit für „setotsa“, gegeben, dass Sepal.Length=6.3 und Setal.Width von 2.5 und Pental.Length von 4.9 und Petal.Width von 1.5 gemessen wurde, ist proportional zur Vorabwahrscheinlichkeit „setosa“ zu beobachten (=33%), multipliziert mit der Wahrscheinlichkeit Sepal.Length = 6.3 bei Gewächs „setosa“ zu beobachten, multipliziert mit der Wahrscheinlichkeit Sepal.Width = 2.5 bei Gewächs „setosa“ zu beobachten, multipliziert mit der Wahrscheinlichkeit Petal.Length = 4.9 bei Gewächs „setosa“ zu beobachten, multipliziert mit der Wahrscheinlichkeit Petal.Width = 1.5 bei Gewächs „setosa“ zu beobachten.
Für den Fall „versicolor“ und „virginica“ ist analog vorzugehen.
Wie kommen wir hierbei zu den Wahrscheinlichkeiten der einzelnen Merkmale, etwa zu „Sepal.Length“? In einem ersten vorbereitenden Schritt werden die Daten wie bereits ausgeführt in eine Trainingsmenge und in eine Testmenge unterteilt. Die Trainingsmenge dient hierbei zu Generierung der Verteilung der einzelnen Merkmale für die drei verschiedenen Gewächse. Der Einfachheit halber wurden die ersten 30 Datensätze als Trainingsmenge und die restlichen 20 Datensätze eines jeden Gewächses als Testmenge herangezogen.
Als weiteres Charakteristikum des Naive Bayes Klassifikator ist die Annahme der Normalverteilung der Merkmale zu erwähnen, wobei hierzu die Mittelwerte und Varianzen aus der Trainingsmenge herangezogen werden (siehe Zellen W14ff. aus Tabellenblatt „Model“).
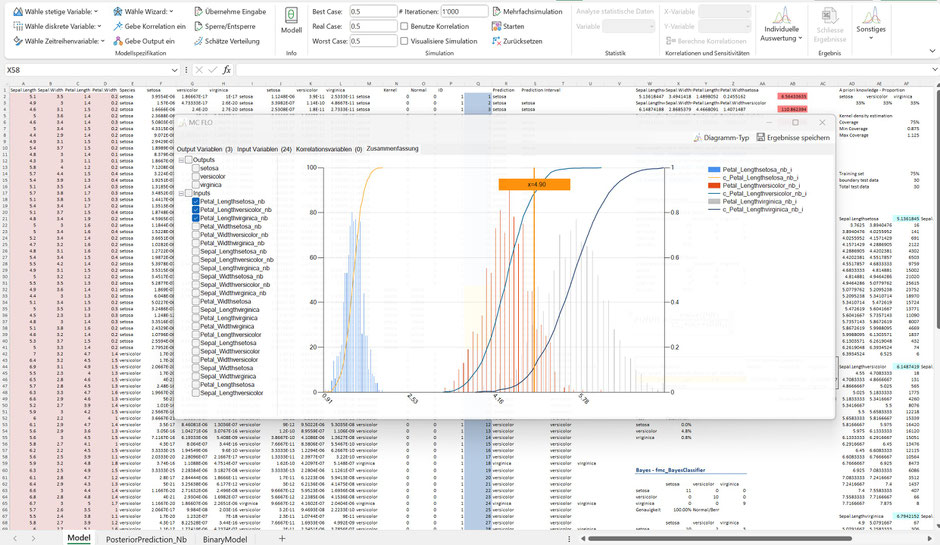
Eine Erweiterung des Naive Bayes Klassifikators berücksichtigt die empirische Verteilung der Trainingsmenge, wobei MC FLO diese anhand eines Kerndichteschätzers herleitet (siehe Zellen AF21ff.). Beide Fälle sind folgend für „Sepal.Length“ des Gewächses „setosa“ zusammengetragen.
Für Petal.Length = 4.9 und unter Beizug der Normalverteilung ist sodann ersichtlich, dass dieser von den Gewächsen „versicolor“ und „verginica“ überdeckt wird, nicht jedoch von „setosa. Allein in Bezug auf das Merkmal „Petal.Length“ und einer beobachteten Merkmalsausprägung von 4.9 würden wir die Zuordnung auf das Gewächs „setosa“ ausschliessen wollen.
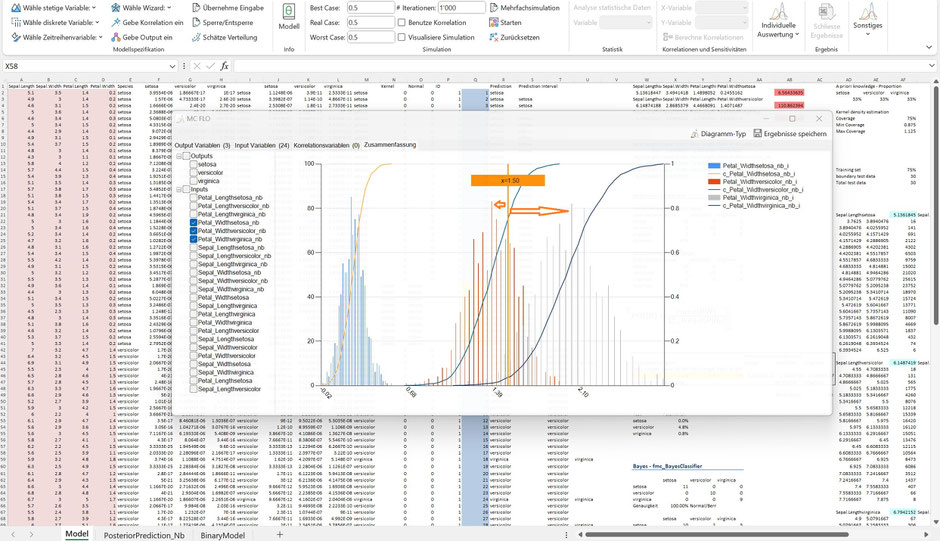
Beim Merkmal „Petal.Width“ bei der beobachteten Grösse von 1.5 fällt auf, dass dieses dem Gewächs „versicolor“ zugeordnet werden sollte, da der Wert von 1.5 näher am Maximum von „versicolor“ als von „virginica“ liegt.
Und siehe da: Das Ergebnis unter Auswertung aller Merkmalsausprägungen zeigt auf, dass unter Zugrundelegung der apriori Verteilung es am wahrscheinlichsten ist, wonach der neue Datensatz dem Gewächs „versicolor“ entstammt.
Bei der Beurteilung ist zu beachten, dass in der Klassifikation nicht die absolute Wahrscheinlichkeit zählt, (siehe Zelle AA46ff), sondern die Zuordnung der ermittelten Wahrscheinlichkeit eines Gewächses relativ zu den anderen Gewächsen. („Bayes-Faktor“). So ist die Wahrscheinlichkeit, dass die gemessenen Daten zu „versicolor“ gehören, 20 mal höher als bei „virginica“ ist.
Dies führt dann zur Frage, wie sicher wir sein können, dass der Datensatz tatsächlich dem Gewächs „versicolor“ entspricht. Die Bayessche Statistik erlaubt unter Rückgriff der jeweiligen Verteilungen und der apriori Wahrscheinlichkeit eine Posteriori Verteilung zu generieren, aus der das Intervall abgeleitet wird. Hierzu werden jeweils zufällige Werte aus den genannten Verteilungen gezogen und das Ergebnis ermittelt (siehe Tabellenblatt „PosteriorPrediction_NB“).
Die für „versicolor“ und „virginica“ ermittelte Wahrscheinlichkeit liegt innerhalb des jeweiligen 95% glaubwürdigen Intervalls. Wollen wir somit ein glaubwürdiges Intervall als Ergebnis angeben, wären im vorliegenden Datensatz die Gewächse „versicolor“ und „virginica“ zu nennen.
Eine generelle Betrachtung anhand der Testmenge zeigt auf, dass der Naive-Bayes Klassifikator auf Basis der Annahme normalverteilter Merkmale eine gleich hohe Genauigkeit (97%) wie das Model auf Basis der empirischen Verteilung aufweist.
In diesem Fall sollte eine Entscheidungsperson indifferent hinsichtlich des auszuwählenden Modells („Modellselektion“) sein. Sobald das Modell ausgewählt ist, ist unter Einschluss der Daten aus der Testmenge das ausgewählte Modell neu zu kalibrieren und dieses für den neuen Datensatz anzuwenden.
Abschliessend soll nächster folgender Datensatz klassifiziert werden:
Sepal.Length = 10
Sepal.Width = 10
Petal.Length=10
Petal.Width=10
Wie ersichtlich ist dieser Datensatz nicht in der Trainingsmenge enthalten: der Wert von 10 wird von keiner der ermittelten Verteilungen der einzelnen Merkmale überdeckt. Was ist somit zu tun? Die einfachste Möglichkeit besteht darin allein die apriori Wahrscheinlichkeit zu nehmen. In diesem Fall sind alle Gewächse gleich wahrscheinlich.
Mit MC FLO ab Version 7.7.4.0 sind die hier beschriebenen Verfahren auch komplett automatisiert verfügbar. In Zelle W62 ist die Wahrheitsmatrix in Bezug auf eine Trainingsmenge von 75% - analog den bisherigen Ausführungen – auf Basis der Normalverteilung abgetragen.
Im Gegensatz zu oben ist die Erkennungsrate in Bezug auf die Testmenge hingegen aber 100%, statt 97%. Zwei Gründe sind für die Differenz verantwortlich. Zum einen wählt der automatisierte Algorithmus die Daten aus der Trainingsmenge zufällig aus, die jeweiligen Mittelwerte und die Standardabweichung können daher von den obigen Ausführungen abweichen. Zum anderen werden für die Generierung der Verteilungen jeweils neue Stichproben – hier 1‘000 - gezogen.
In Zelle W68 wird anhand eines Kerndichteschätzers eine Klassifikation vorgenommen und die entsprechende Wahrheitsmatrix ausgewiesen.
Beim Kerndichteschätzer können Minimal- und Maximalwerte definiert werden, diese werden prozentual auf den Minimal und Maximalwerte der Trainingsdaten angesetzt. Im obigen Beispiel ist ein Maximalwert von 1.08 definiert. Falls der grösste Wert aus den Trainingsdaten 10 betrüge, dann wäre der Maximalwert beim Kerndichteschätzer 10.8 (10*1.08).
In Zelle R2ff wird statt eine Wahrheitsmatrix eine Punktprognose auf Basis der Normalverteilungsannahme ermittelt.
Abschliessend wird in Zelle S2ff ein Prognoseintervall auf Basis des 90% Sicherheitsniveaus dargestellt.
Wie ersichtlich sind einige Zeile leer – in Bezug auf das 90% glaubwürdige Intervall kann keines der Gewächse mit den Merkmalsausprägungen der entsprechenden Zeile in Verbindung gebracht werden. Soll mindestens ein Gewächs je Zeile identifiziert werden, wäre das glaubwürdige Intervall zu erhöhen.
Auch wenn das vorgestellte Beispiel der Schwertlinien langweilig klingen mag, die Anwendungsbreite des Naive Klassifikators ist nahezu unerschöpflich. Stellen Sie sich vor, dass Sie die Möglichkeit eines Kreditausfalls ihres Unternehmens zu berechnen haben und hierzu Daten von anderen Unternehmen in Bezug auf relevante Kennzahlen (EBIT-Marge, EK/FK Quote etc.) und den Kreditausfall („Ja“, „Nein“) haben. Mit dem Bayes Klassifikator ist es nun ein Kinderspiel zu identifizieren, ob ihr Unternehmen wahrscheinlich von einem Kreditausfall betroffen sein wird oder nicht.
P.S.: Im Vergleich zu einer Regression kommt eine Klassifikation dann zu Einsatz, wenn der Output nicht als numerischer Wert, sondern als Kategorie vorliegt. Sie können aber ein Regressionsproblem auch in ein Klassifikationsproblem überführen (und umgekehrt). So können Sie beispielsweise Werte zwischen 1 und 10 in „geringe Kreditausfallwahrscheinlichkeit“, Werte zwischen 10 und 20 in „hohe Kreditausfallwahrscheinlichkeit“ transformieren und dann die Klassifikation durchführen. Zwar haben Sie mit diesem Vorgehen einen Informationsverlust, für viele Fragestellungen ist dieser aber verhältnismässig.
Info: Das Modellbeispiel enthält viele volatile Funktionen, welche die Performance stark beinträchtigen. Wir empfehlen das Modellbeispiel mit maximal 1‘000 Iterationen durchzuführen. Mit Rückgriff allein auf die automatisierten Funktionen ist die Performance hingegen deutlich besser. Zudem gilt zu beachten, dass mit jedem neuen Aufruf der automatisierten Funktionen leicht geänderte Ergebnisse resultieren können, was auf das Aufrufen des Zufallsgenerators zurückgeführt werden kann. Der in MC FLO verwendete Klassifikationsalgorithmus verwendet die Summe der Vorabwahrscheinlichkeit und der Likelihood, beides auf Basis logarithmierter Werte. Falls keine Wahrscheinlichkeit ermitellt werden kann, wird ein Default Wert von 0.000000001 angesetzt,.
















Kommentar schreiben