Während wir in einem der letzten Blogs die Bayessche Klassifikation («Naive Bayes Klassifikator») vorgestellt haben, wollen wir uns hier auf die Bayessche lineare Regression fokussieren.
Die Regressionsanalyse ist ein statistisches Verfahren, mit dem versucht wird eine beobachtete abhängige Variable durch eine oder mehrere unabhängige Variablen zu erklären. Bei der linearen Regression wird dabei ein lineares Modell angenommen. Es werden also solche Zusammenhänge herangezogen, bei denen die abhängige Variable eine Linearkombination der unabhängigen Variablen ist; klassisch im Fall der einfachen linearen Regression ausgedrückt: y = Achsenabschnitt(a) + Steigungsparameter(b) * Ausprägung der unabhängigen Variable (x); y = a + b*x. Ist beispielsweise der Achsenabschnitt = 2, der Steigungsparameter = 3, dann führt der Wert 4 für die unabhängige Variable zu einem geschätzten durchschnittlichen Wert von 14 für die abhängige Variable y; y = 2 + 3 * 4 = 14. Bei einem Wert von 5 für x resultiert ein geschätzter durchschnittlicher Wert von 17 für y. Für jeden neuen Wert von x steigt y linear um 3 Einheiten an. y wird somit durch x erklärt. Warum der Begriff «geschätzter, durchschnittlicher Wert»? Zum einen wollen wir y voraussagen und nicht nur beobachten. Zum anderen wird es so sein, dass die Regressionsgerade den Durchschnitt der möglichen y Werte durchquert. Im Regelfall werden die tatsächlichen Realisierungen aber um den Durchschnitt streuen. In der klassischen, lineare Regression wird angenommen, dass diese Streuung normalverteilt ist.
Wie kommen wir nun zu der Bayesschen linearen Regression? Nun, die Bayesschen Statistik geht wie bereits mehrfach ausgeführt von einem Vorwissen hinsichtlich der relevanten Parameter – hier der Regressionsparameter «a» und «b» - aus, dieses Wissen wird anhand beobachteter Daten geschärft, um dann anhand des Satzes von Bayes Aussagen zu möglichen zukünftigen Realisierungen zu treffen.
Dass die Bayessche Regression höchst praxisrelevant ist, wird am folgenden Beispiel ersichtlich:
Ein Unternehmen möchte ein exklusives, elektrisches Gefährt für Menschen mit beschränkter Mobilität auf dem Markt lancieren. Hierzu wurden bereits verschiedene Markterhebungen durchgeführt, um mögliche Absatzmengen und Absatzpreise zu eruieren. Die Produktionsabteilung ist nun beauftragt worden eine Aufwandsschätzung für verschiedene Absatzmengen aufzustellen, welche für die Herleitung des Deckungsbeitrags und somit als Entscheidungsgrundlage für die Lancierung des neuen Produktes dienen soll. Dabei soll die Performance der Aufwandsschätzung auch als Mass für die variable Vergütung der Produktionsabteilung und die Regression als Messinstrument für die zukünftige Aufwandsprognose auf Basis der hergestellten Einheiten herangezogen werden. Das Management und die Produktionsabteilung verständigen sich den Zusammenhang zwischen produzierten Einheiten und dem Aufwand anhand einer einfachen linearen Regression zu beschreiben und den Aufwand auf wöchentlicher Basis zu ermitteln; y (Aufwand) = fixer Aufwand (a) + «Steigungsparameter» (b) * x (Anzahl produzierter Einheiten). Der Aufwand hängt somit von einem fixen Betrag, dem Steigungsparameter und der Anzahl produzierter Einheiten linear ab*.
Ohne Kenntnis von beobachteten Daten ist im Sinne der Bayesschen Statistik auf Vorwissen für die Modellgrössen «fixer Aufwand» und «Steigungsparameter» abzustützen. So kann die Produktionsabteilung anhand eigener Erfahrungen eine Schätzung über die Modellgrössen vornehmen. Alternativ kann über Treibermodelle, welche den Produktionsprozess in die einzelnen Bestandteile zerlegen, eine Aufwandsschätzung aufgestellt und in eine Regressionsgleichung überführt werden.
Aufgrund der vielen Treiber, welche mit der Absatzmengen in Zusammenhang gebracht werden können (Materialpreise, Strompreise etc.), sind die Ausprägungen der Treibergrössen unsicher und somit nicht fix. Die Produktionsabteilung gelangt anhand des Treibermodells zur Erkenntnis, dass der variable Aufwand («Steigungsparameter», im Modell als «Slope» bezeichnet) als Normalverteilung mit einem Erwartungswert von 3’500 CHF und einer Standardabweichung von 500 CHF pro Stück ausgedrückt werden kann.
Mit jeder produzierten Einheit fällt somit zusätzlich ein Aufwand von durchschnittlich 3'500 CHF an. Der variable Aufwand kann aufgrund der Unsicherheit aber auch zwischen 2'500 und 4'500 CHF pro Einheit schwanken (siehe Angaben zum 95%-glaubwürdigen Intervall).
Neben den variablen Aufwand ist der fixe Aufwand zu bestimmen (im Modell als «Intercept» bezeichnet), dieser fällt unabhängig von der Absatzmenge an. Die Bestimmung dieser Grösse kann auch hier über verschiedene Wege erfolgen. Sachlogisch konsistent gehen wir davon aus, dass der fixen Aufwand positiv ist (Mieten, Abschreibungen der Maschinen etc.). Da das Design der neuen Fabrik noch nicht abschliessend definiert ist, ist auch hier von Unsicherheit auszugehen. Das Treibermodell ermittelt hierbei - je nach unterstellter Modellausprägung, etwa anhand einer separaten Monte-Carlo Simulation - einen Erwartungswert von 200'000 CHF pro Woche, mit einer Standardabweichung von 35’000 CHF. Die Planungsverantwortlichen gehen somit davon aus, dass der fixe Aufwand aufgrund der Unsicherheit zwischen 132'000 CHF und 269'000 CHF pro Woche schwanken kann.
Nachdem wir mögliche Werte für den «typischen» fixen («Achsenabschnitt») und den variablen Aufwand definiert haben, lassen sich mögliche Regressionsgeraden simulieren, respektive «generieren» (daher auch der Name der «generativen Modelle»).
So sehen wir, dass bei einer Produktionsmenge von 52 Einheiten in der Woche, der durchschnittliche Aufwand (im Modell mit «Simulated_Prior_Line_52» bezeichnet) im 95%-Intervall zwischen ca. 298'000 und ca. 468'000 CHF / Woche liegen kann. Mit zunehmender Produktionsmenge steigen die Kosten an. Bei der angenommenen maximalen Produktionsmenge von 88 Einheiten pro Woche schwankt der durchschnittliche Aufwand zwischen ca. 390'000 und 610'000 CHF pro Woche anhand 9 möglicher Regressionsgeraden.
Im Regelfall werden die gemessenen Punkte nicht auf einer dieser möglichen Regressionsgerade liegen, sondern um diese streuen. Diese Streuung lässt sich nicht durch das Treibermodell «erklären» (etwa Streiks bei Zulieferer etc.) und liegen deshalb ausserhalb der Modellspezifikation und stellen den Standardfehler der Regressionsgeraden dar. Und auch hier kann eine Schätzung vorgenommen werden. Die Verantwortlichen gehen davon aus, dass der durchschnittliche Schätzfehler zwischen 60'000 CHF und 90'000 CHF mit einem Erwartungswert von 75'000 CHF schwankt (im Modell als «RE» bezeichnet). Im Gegensatz etwa zum «Steigungsparameter» haben die Produktionsverantwortlichen keine Präferenz, welche Werte eher wahrscheinlicher sind, womit eine Gleichverteilung als initiale Planungsprämisse resultiert.
Anhand der vorliegenden spezifizierten Angaben zu den fixen, variablem Aufwand und dem Standardfehler können mögliche Aufwände anhand der Produktionsmengen simuliert werden. Hierzu wird zufällig ein Wert aus den jeweiligen unsicheren Grössen herangezogen und anhand der Produktionsmenge der Aufwandsanfall ermittelt.
Für eine Produktionsmenge von 52 Einheiten resultiert ein geschätzter Aufwand von ca. 382'000 CHF pro Woche. Aufgrund der Stichprobenvariabilität kann dieser Aufwand mit 95%-iger Sicherheit aber auch zwischen ca. 211'000 CHF und 554'000 CHF liegen (siehe Angaben zu «Simulated_Prior_52»).
Um die Rentabilität zu ermitteln, sind ausgehend vom Absatzpreis (10'000 CHF pro Stück) und einer angenommenen Produktionsmenge pro Woche (welche PERT-verteilt mit einem Erwartungswert von 52 Einheiten und einem Maximalwert von 88 Einheiten pro Woche ist, siehe «Data_prior») die simulierten Produktionskosten je Einheit und somit die Marge («Margin») zu ermitteln. Bei einer Produktionsmenge von durchschnittlich 52 Einheiten pro Woche schwankt die Marge zwischen ca. -132'000 CHF und 400'000 CHF. Die Marge liegt im Erwartungswert – vor Beobachtung konkreter Daten – bei ca. 138’000 CHF.
Anhand der simulierten Zahlen kann nun die Wahrscheinlichkeit ermittelt werden, mit welchem der Umsatz unter dem Aufwand liegt. Diese beträgt ca. 16.4% (Zelle C20). Das Management kann nun risikoorientiert anhand der Daten aus der Simulation entscheiden, ob es die Produktion aufnimmt und somit das Produkt lanciert.
Die klassische, frequentistische Statistik macht Schlussfolgerungen nur anhand von gemessenen Daten, womit die bisher gemachten Ausführungen in der klassischen Statistik nicht möglich sind (insbesondere wenn davon auszugehen ist, dass das hier betrachtete Unternehmen nicht mit anderen vergleichbar ist). Das ist der Vorteil von Bayesschen Verfahren und speziell von generativen Modellen, da sie auf Verteilungen aufbauen und somit in der Lage sind «Vorwissen» messbar zu machen.
Nach Erstellung der Fabrikanlage und Produktion der elektrischen Gefährte liegen im Zeitverlauf tatsächliche und nicht nur rein simulierte Werte vor. Das Unternehmen kann nun diese (wenige) Zahlen heranziehen und mit dem Vorwissen kombinieren, um daraus neue Aufwandsschätzungen abzuleiten. Schliesslich kann das Management messen, wie «gut» das Treibermodell und somit die Prognose im Vergleich zu den gemessenen Daten abschneidet.
Folgende Daten aus den ersten zehn Wochen sollen zur Prüfung des Modells und für neue Prognosen herangezogen werden (wir ignorieren Lerneffekte; alternativ ist auf eine Zufallsstichprobe nach Hochlauf abzustützen; zudem gehen wir davon aus, dass die produzierten Mengen nur auf Nachfrage erstellt werden, womit der Aufwand für die Lagerhaltung entfällt):
| Week | Items | Expenses (in CHF) |
| 1 | 10 | 240'718 |
| 2 | 31 | 416'122 |
| 3 | 64 | 376'824 |
| 4 | 6 | 261'964 |
| 5 | 43 | 413'744 |
| 6 | 87 | 562'149 |
| 7 | 34 | 414'239 |
| 8 | 22 | 249'909 |
| 9 | 65 | 502'280 |
| 10 | 33 | 450'753 |
Sowohl in der frequentistischen als auch in der Bayesschen Statistik wird unterstellt, dass die Daten einem Prozess folgen. In MC FLO wird anhand von bootstrap dieser Prozess simuliert, dabei werden die gemessenen Daten zufällig neu «gewürfelt» (Stichprobenziehung) und die resultierende Regressionsgerade bestimmt. Anhand von tausenden Stichprobenziehungen wird eine Verteilung der gesuchten Parameter (Achsenabschnitt, Steigungsparameter, Standardfehler) generiert. Diese stellt dann die Likelihood (Plausibilität) der einzelnen Parameter dar.
Für den Steigungsparameter wird anhand des bootstrap Verfahrens ein Aufwand zwischen ca. 2’100 CHF und 5’800 CHF pro Stück im 95%-Intervall geschätzt. Für den Achsenabschnitt resultiert ein Prognoseband von 200'000 CHF bis 349'000 CHF. Für den Standardfehler resultieren Werte zwischen ca. 63'000 CHF und 100'000 CHF.
Wichtig ist zu betonen, dass die Likelihood einen Prozess beschreibt und im Sinne der frequentistischen Interpretation keine Aussage zum «wahren» Wert eines Parameter – wie dem Achsenabschnitt – zulässt.
So wird anhand des Data Analysis Tools von Microsoft Excel für den Achsenabschnitt («Intercept») mit der frequentistischen Methode ein Koeffizient von ca. 249'000 CHF ermittelt, was sehr nah am oben genannten Wert von 260'000 CHF anhand des bootstrap Verfahrens zu liegen kommt; das Konfidenzintervall liegt dabei bei ca. 162'000 CHF und ca. 335'000 CHF. Nun darf daraus aber nicht der Schluss gezogen werden, dass der «wahre» Achsenabschnitt vom Konfidenzintervall überdeckt wird. Diese Schlussfolgerung lässt der frequentistische Ansatz leider nicht zu. Erst die Kombination des Vorwissens mit der Likelihood anhand des Satzes von Bayes erlaubt eine Aussage zur Überdeckung. Doch dazu gleich mehr.
Um es klar zu sagen: Da es sich um Stichproben handelt, lassen sich keine Beweise aufstellen. Die Datenlage kann somit nur als Indiz dienen. Die ermittelten Konfidenzintervalle lassen aber durchaus den Schluss zu, dass das Vorwissen kompatibel mit den gemessenen Daten sind.
Von der frequentistischen Statistik wird oft der Vorwurf erhoben, dass das Abstützen auf ein Vorwissen die gemessenen Daten «verwässert», womit verzerrte Entscheidungsgrundlagen resultieren. Somit dürfe nur auf die Likelihood abgestützt werden («let the data speak»). Wir bei MC FLOsim sehen das differenzierter. Was wenn die gemessenen Daten noch nicht die ganze Wahrheit widerspiegeln? Zudem sind Daten ohne Kontext nutzlos und somit zu bewerten. Eine Bewertung unterliegt aber subjektiven Einschätzungen, womit der postulierte objektive Massstab eine Utopie darstellt. Schliesslich kann nur durch Kombination des Vorwissens mit der Likelihood eine glaubwürdige Aussage zum «wahren» Parameter getroffen werden, denn es gilt: P(H|D)∝("ist proportional zu")P(D|H)*P(H), wobei P(H) unser Vorwissen und P(D|H) das Ergebnis der Likelihood darstellt. P(H|D) ist die gesuchte Grösse, die Wahrscheinlichkeit H zu beobachten, gegeben, dass die Daten D vorliegen. P(H|D) liegt als Verteilung vor und wird als Posterior-Verteilung bezeichnet.
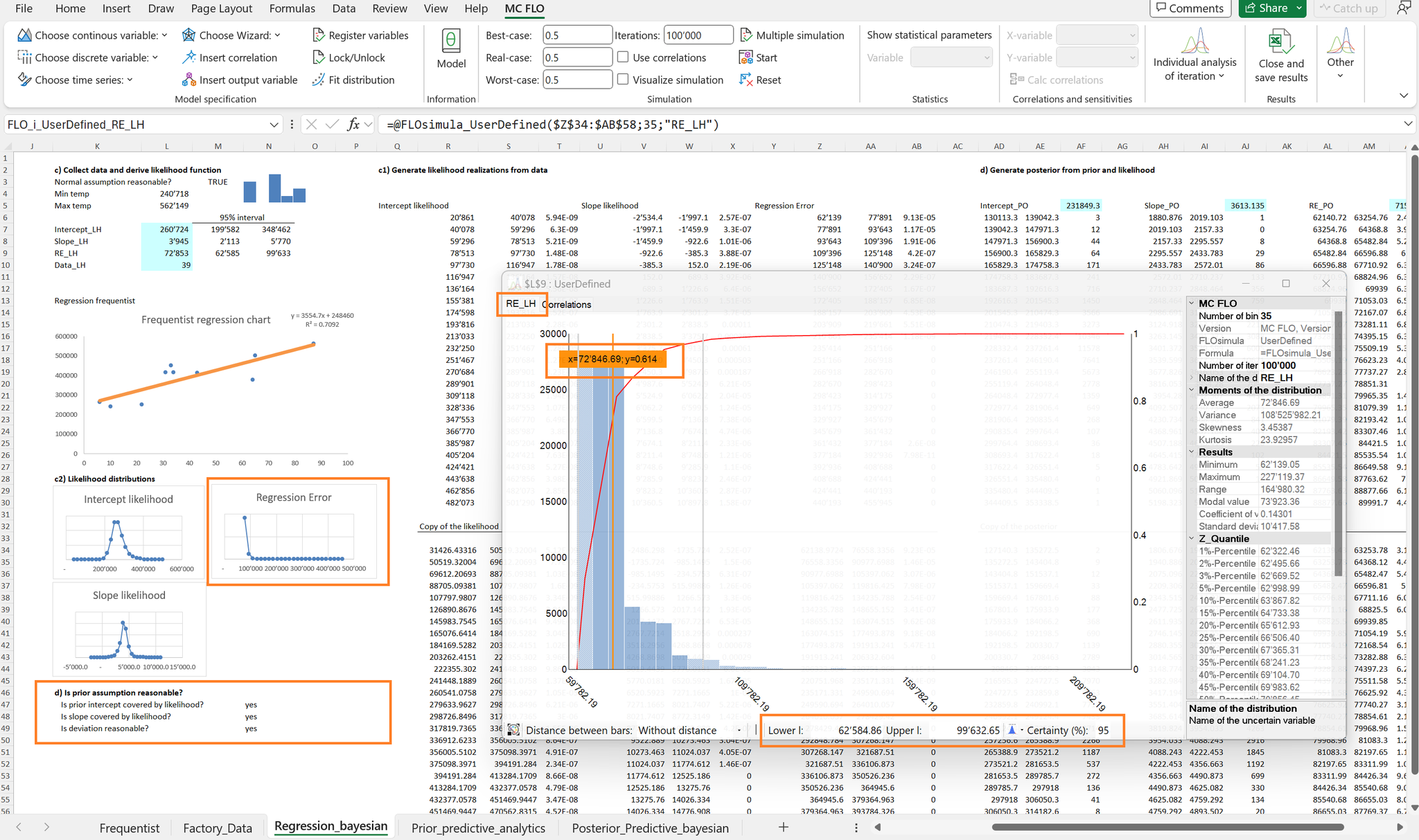
Durch Kombination des Vorwissens mit der Likelihood können wir ein angepasstes Wissen herleiten, welches die gemessenen Daten für eine neue Prognose beizieht (die Modellparameter sind mit der Endung «_PO» für «Posterior» ersichtlich).
Durch die Technik des Markov-Chain Monte Carlo (MCMC) kann P(H|D) approximativ bestimmt werden. Für den Achsenabschnitt oder auch den fixen Aufwand wird mit MCMC ein Wert von ca. 232’000CHF ermittelt, wir können uns dabei zu 95% sicher sein, dass der wahre fixe Aufwand zwischen 190’000 CHF und 272’000 CHF pro Woche liegt. Für den Steigungsparameter resultiert ein Erwartungswert von ca. 3'600 CHF pro Einheit und der Standardfehler der Regression liegt im Erwartungswert bei ca. 71'000 CHF. Die Ergebnisse liegen sehr nah an der Likelihood, was aufgrund der breiten Streuung des Vorwissen zurückgeführt werden kann. Aber noch einmal: Das ist kein Beweis dafür, dass alle zukünftigen Daten innerhalb der gemessenen Intervalle liegen werden. Sollte eine weitere Messung komplett andere Zahlen herausspucken, dann resultieren neue Likelihoods und folglich angepasste Posteriorverteilungen, womit der «wahre» Parameter in einem neuen Lichte erscheinen dürfte. Dies ist im Sinne der Bayesschen Statistik nicht verwerflich, sondern Resultat eines Lernprozesses, wie er Neudeutsch unter dem Pseudonym des «Künstlichen Intelligenz» breit verankert ist.
Anhand der verschiedenen Posteriorverteilungen für die Parameter der Regressionsgleichung lassen sich nun konsistente Aussagen zum typischen Aufwand und zur Prognose des Aufwands einer bestimmten Anzahl produzierter Einheiten erstellen. Fangen wir mit Ersterem an: «Wie hoch wird der durchschnittliche, typische Aufwand bei 52 produzierten Einheiten sein?» Der typische Aufwand bei produzierten Einheiten von 52 Stück liegt bei ca. 420'000 CHF. Aufgrund der Unsicherheit bei «Achsenabschnitt» und «Steigungsparameter» kann der typische Aufwand aber auch zwischen ca. 367'000 CHF und 474'000 CHF liegen (siehe 95% glaubwürdige Intervall). Die Antwort zur Frage: «Wie hoch wird der Aufwand bei produzierten 52 Einheiten sein?» ist differenzierter, da nicht auf den typischen, durchschnittlichen Aufwand von allen möglichen 52 Einheiten abgestützt wird, sondern von einer individuellen Beobachtung. Zusätzlich zur Parameterunsicherheit ist hierbei die Stichprobenvariabilität zu berücksichtigen. Im 95% glaubwürdigen Intervall liegt der Aufwand bei einer individuellen Prognose von 52 Einheiten zwischen 270'000 CHF und 571'000 CHF. Das glaubwürdige Intervall ist hier somit breiter als bei der Prognose des typischen Aufwands. Um das Modell weiter zu validieren ist sind Posteriorverteilung auf die gemessenen Daten anzuwenden. Von allen 10 gemessenen Datenpunkten ist der entsprechende Aufwand im jeweiligen 95%-glaubwürden Intervall enthalten.
Da im Modell nicht nur die Regressionsparameter, sondern auch die Nachfrage, respektive die produzierten Einheiten einer erneuten Prognose unterzogen werden können, ist die Marge bei dem angenommenen Verkaufspreis von 10'000 CHF pro Einheit neu zu beurteilen. Auch ist aufgrund der beobachteten Daten vorgängig eine Posteriorverteilung der Absatzmenge pro Woche herzuleiten, wobei hierbei auf eine Kerndichteschätzung abgestützt wurde. Der Vorteil eines Kerndichteschätzers ist, dass datengenerierenden Prozesse simuliert werden können, welche nicht von den klassischen Verteilungen (etwa Normalverteilung, Gammaverteilungen etc.) eingefangen werden können. Unter Rückgriff die angepassten Produktionsmengen je Woche kann die Marge erneut beurteilt werden. Diese liegt neu im Erwartungswert bei ca. 10'000 CHF in der Woche. Die Wahrscheinlichkeit in der nächsten Woche unter Rückgriff der Regressionsrechnung eine Marge kleiner < 0 CHF zu erwirtschaften beträgt neu ca. 48%. Wie ersichtlich liegt die durchschnittlich Absatzmenge von knapp 40 Einheiten je Woche deutlich unter der erwarteten Zielvorgabe von 52 Einheiten. Das Problem ist somit nicht die Aufwandsschätzung, sondern der fehlende Absatz.
Fazit: Die Bayessche Regression stellt das notwendige Grundgerüst bereit, um Vorwissen zu Beziehungen einer oder mehrere unabhängigen Variablen zu einer Zielvariablen einer Überprüfung zu unterziehen und Entscheidungen unter Unsicherheit zu begünstigen.
Info: Das hier Vorgestellte und weitere Beispiele werden in der nächsten Version von MC FLO bereit gestellt. Schreiben Sie uns, falls Sie weitere Anregungen haben. Teaser: Wir werden auch nicht volatile Funktionen bereit stellen, um in Microsoft Excel rasch (rascher als mittels Python oder R) eine Bayessche Regression vornehmen zu können.
*Die lineare Regression setzt voraus, dass die Residuen (Abweichungen vom geschätzten Wert vom gemessenen Wert) normalverteilt mit Erwartungswert 0 und «unkorreliert» sind. Ebenfalls wird unterstellt, dass die Varianz über den gesamtem Datenbereich gleich gross ist. Schliesslich wird angenommen, dass die zu bestimmenden Parameter (Achsenabschnitt, Steigung, Standardfehler) unabhängig sind.



























Kommentar schreiben