07. Januar 2024
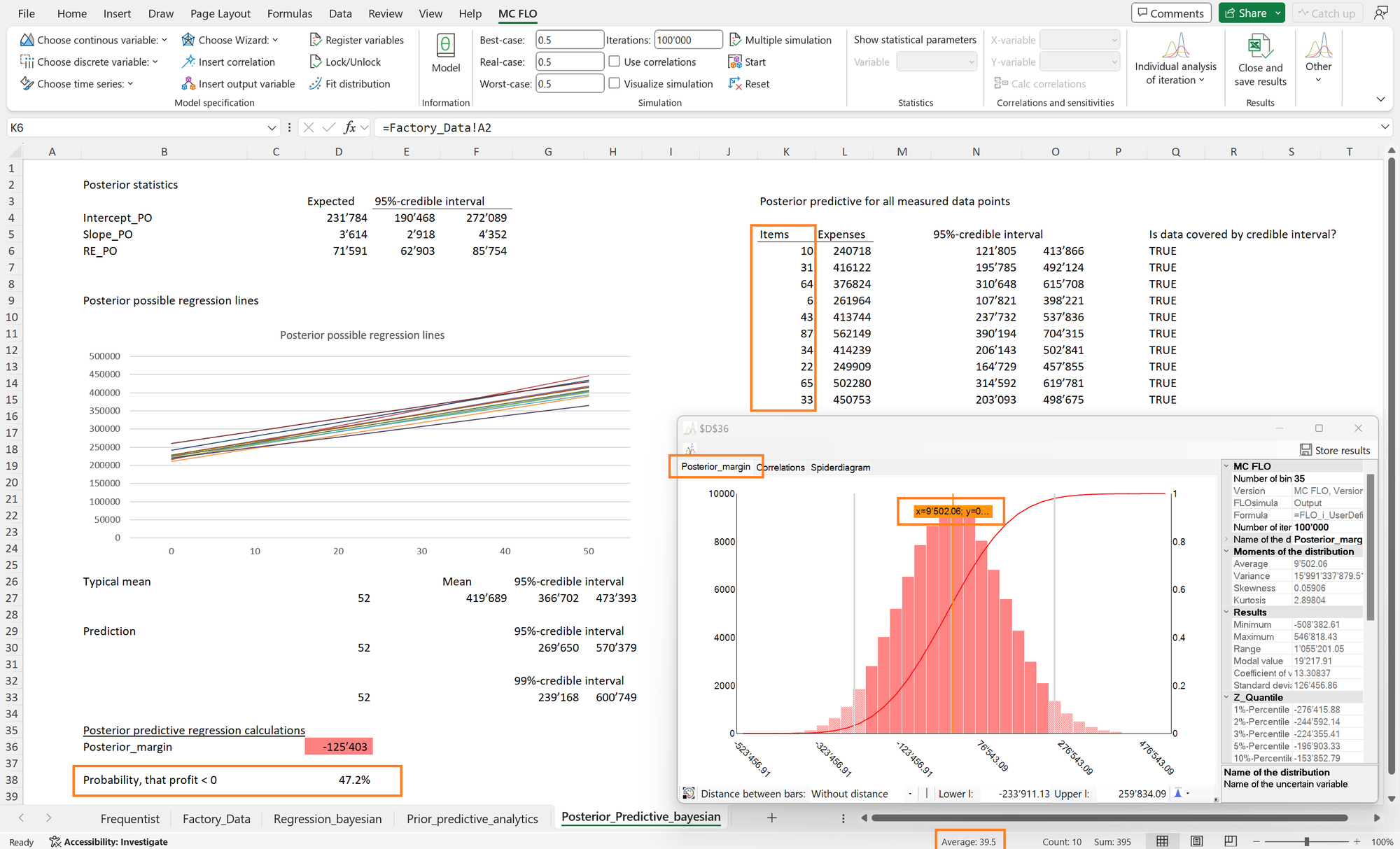
Die Bayessche Regression stellt das notwendige Grundgerüst bereit, um Vorwissen zu Beziehungen einer oder mehrere unabhängigen Variablen zu einer Zielvariablen einer Überprüfung zu unterziehen und Entscheidungen unter Unsicherheit zu begünstigen.
07. August 2023
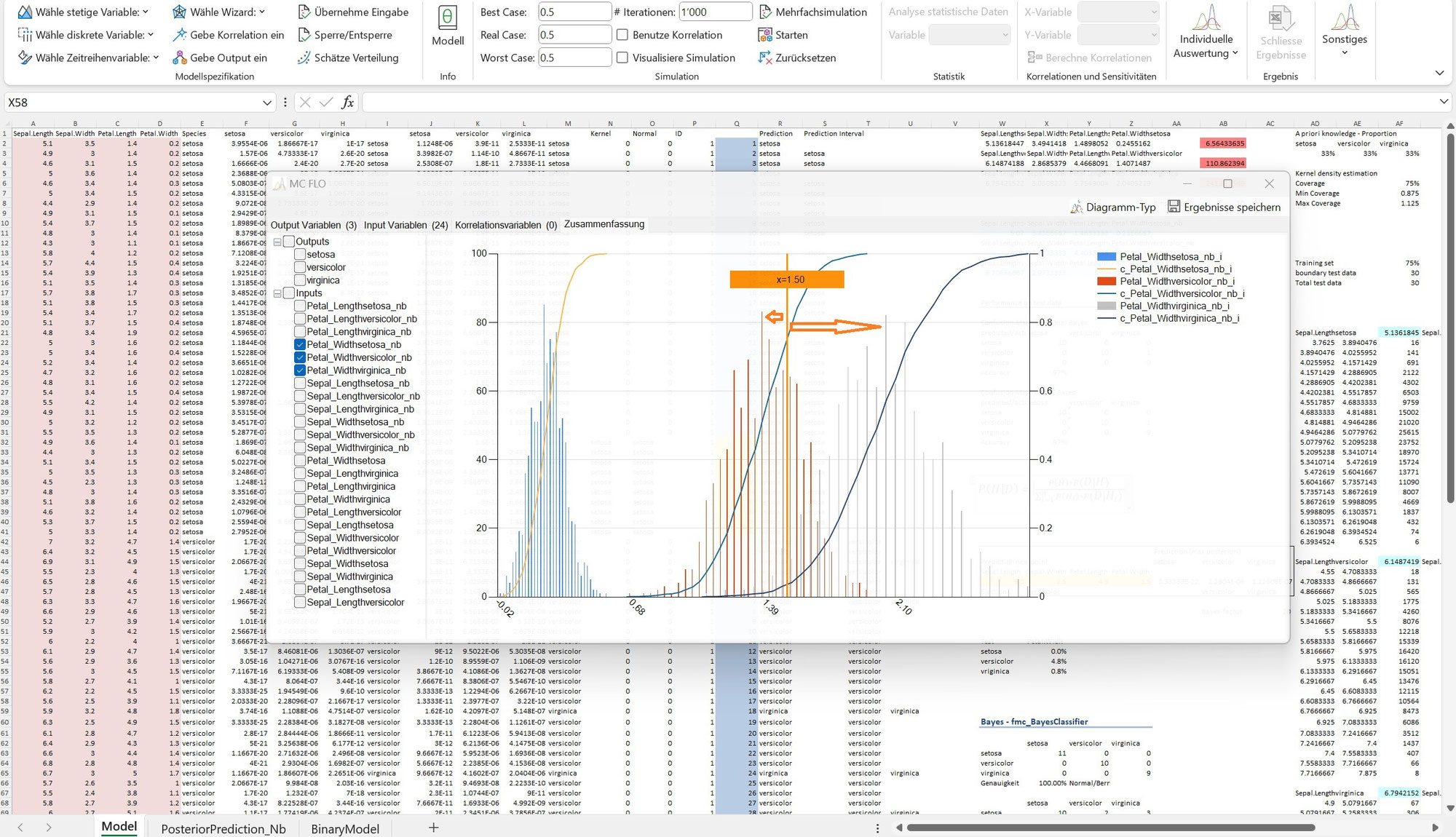
Im Gegensatz zu klassischen Regressionsmodellen, welche Grenzen im Datenraum ziehen und somit zu den diskriminierenden Modellen gezählt werden, verstehen sich generative Modelle – wie der Naive Bayes Klassifikator und ChatGPT – als solche, welche Daten mittels Verteilungen zusammenfassen und somit in der Lage sind neue Daten zu simulieren.
20. März 2023
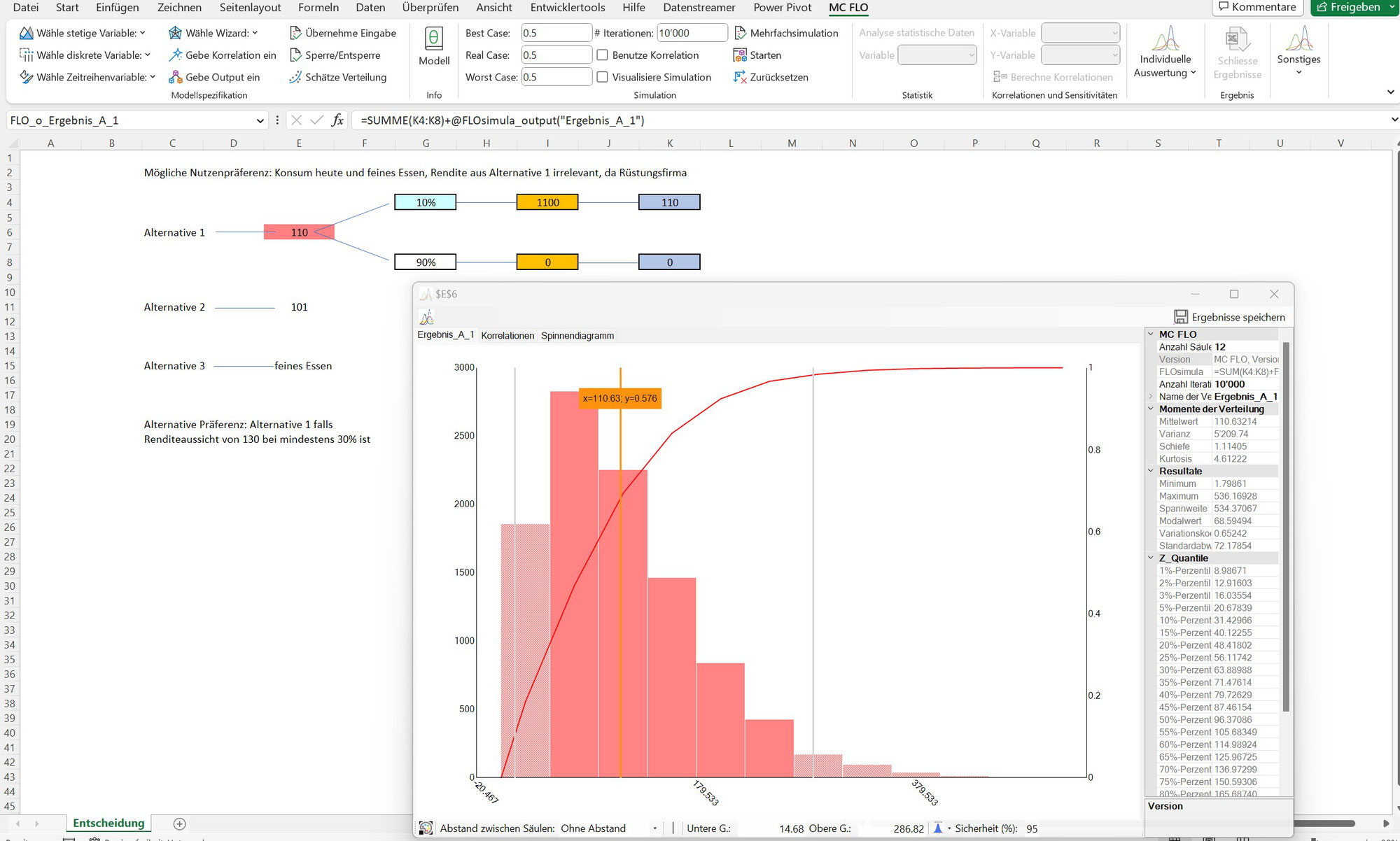
Die prozessorientierte Prognose unter Beizug einer Monte-Carlo Simulation ist Voraussetzung für einen ambitionierten Zielwert. Ist der Zielwert festgelegt, sind alle davon abgeleitete Grössen reine «davon» Planungen. Durch Kombination der Annahmen aus dem Plan und den gemessenen Daten ist eine neue Prognose zu erstellen und der Zielwert gegebenenfalls zu schärfen.
12. März 2023
Bei Prozessen und Daten welche sich nur zögerlich verändern oder gar über den Zeitablauf ein immer gleiches Muster aufweisen, sind klassische Instrumente wie Regressionen ein Segen. In Fällen, in denen weder Wahrscheinlichkeiten noch alle Umweltzustände in ein Modell aufgenommen werden können, scheitern diese jedoch, weil sie das Momentum – den Thanksgiving-Day oder auch den Schwarzen Schwan – nicht antizipieren können.
05. Juli 2021
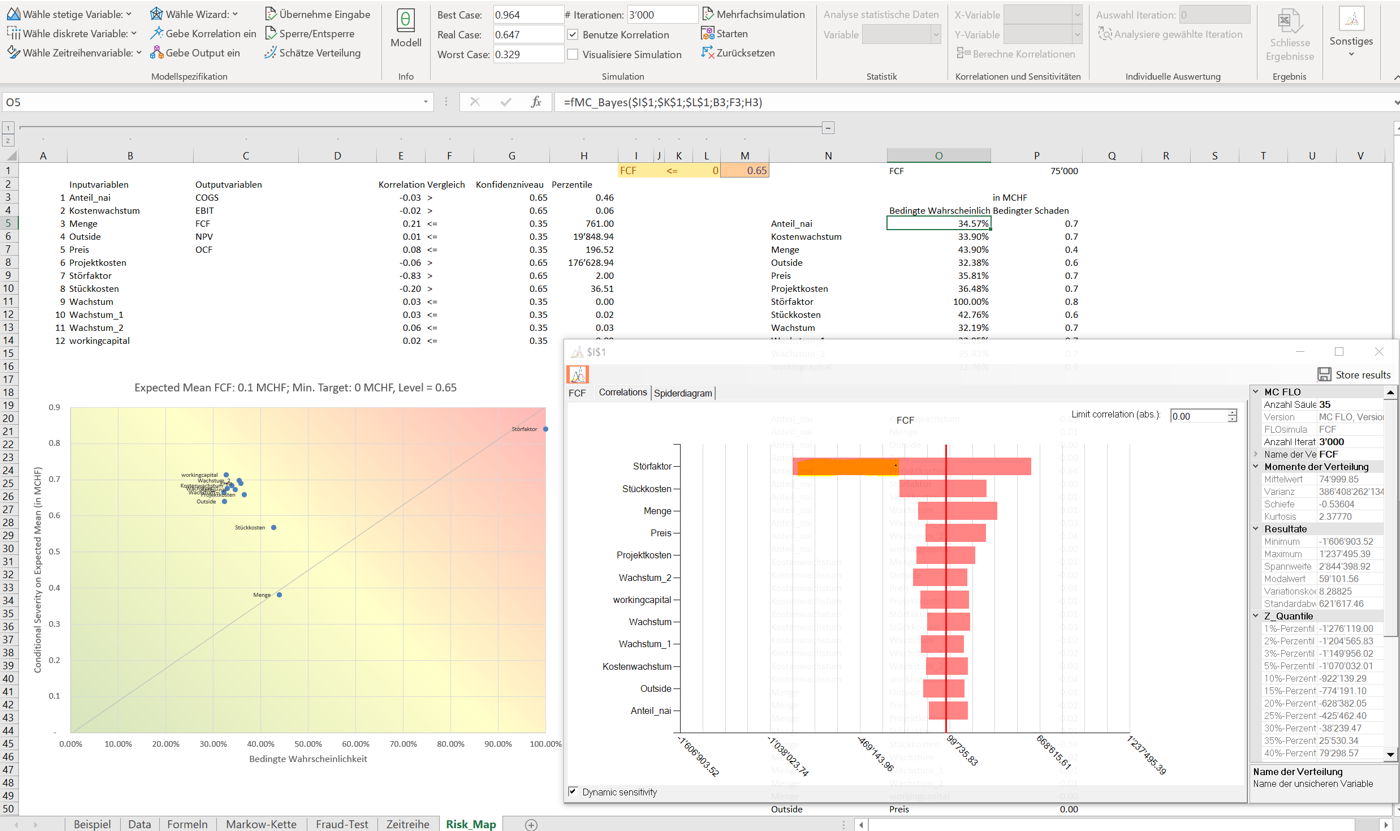
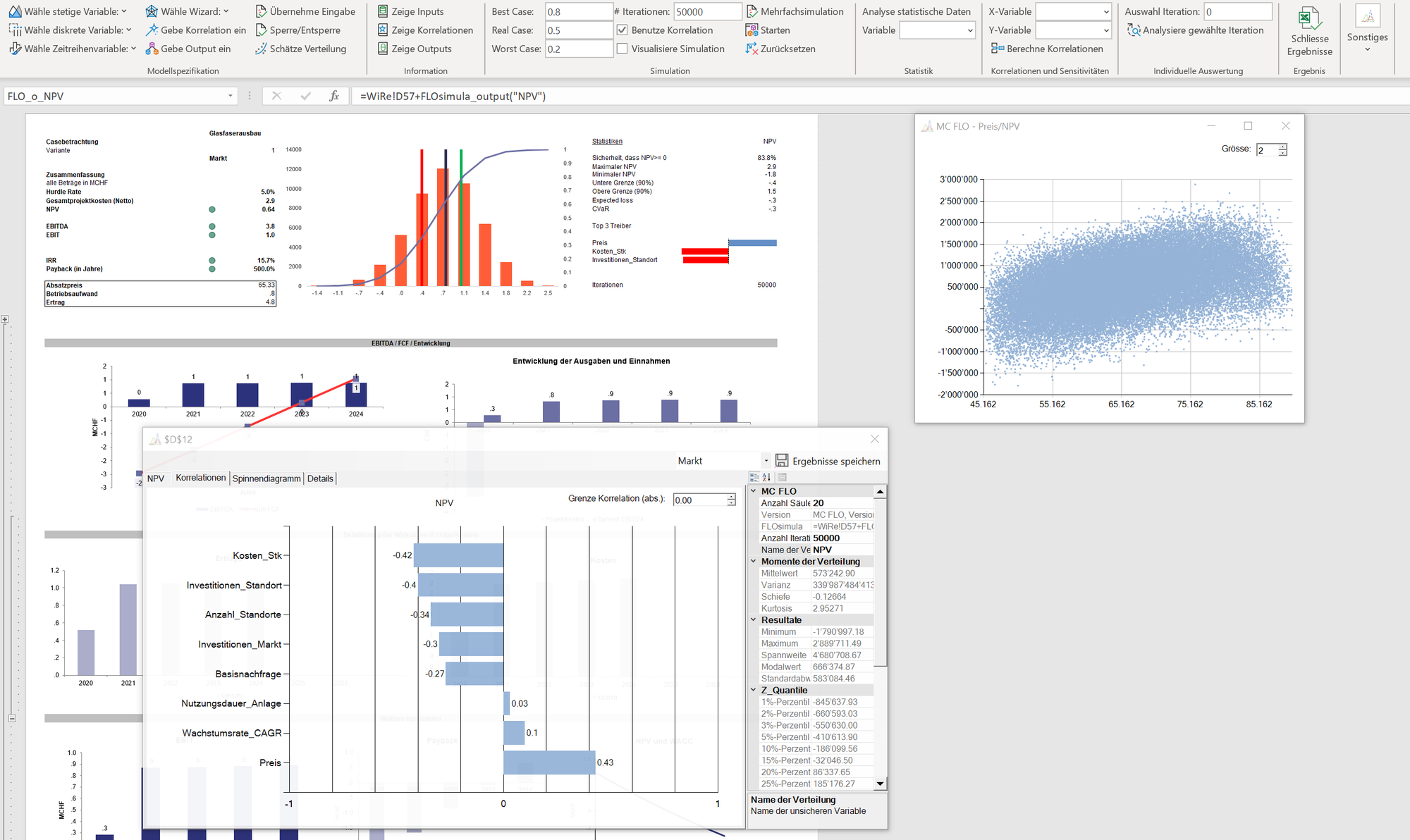
Ziel einer umfassenden quantitativen Analyse mittels Monte-Carlo Simulation ist eine objektiv begründbare Entscheidungsempfehlung unter Berücksichtigung von Unsicherheit, etwa bei den Absatzmengen oder Anzahl Cyberangriffe, welches ein Unternehmen ausgesetzt ist. Für diejenigen Personen, die eine quantitative Analyse schätzen, die Resultate davon aber in einer Risikomatrix abzubilden haben, stehen in MC FLO nun die geeigneten Instrumente bereit.
24. März 2021
Während die gängigen Optimierungsverfahren wie der Simplex-Algorithmus rasch exakte Lösungen liefern können, da sie auf deterministische Ausgangsbedingungen aufsetzen, besticht die Monte-Carlo Simulation durch den Ausweis von Wahrscheinlichkeiten. Das ist der Kern.
20. Februar 2020
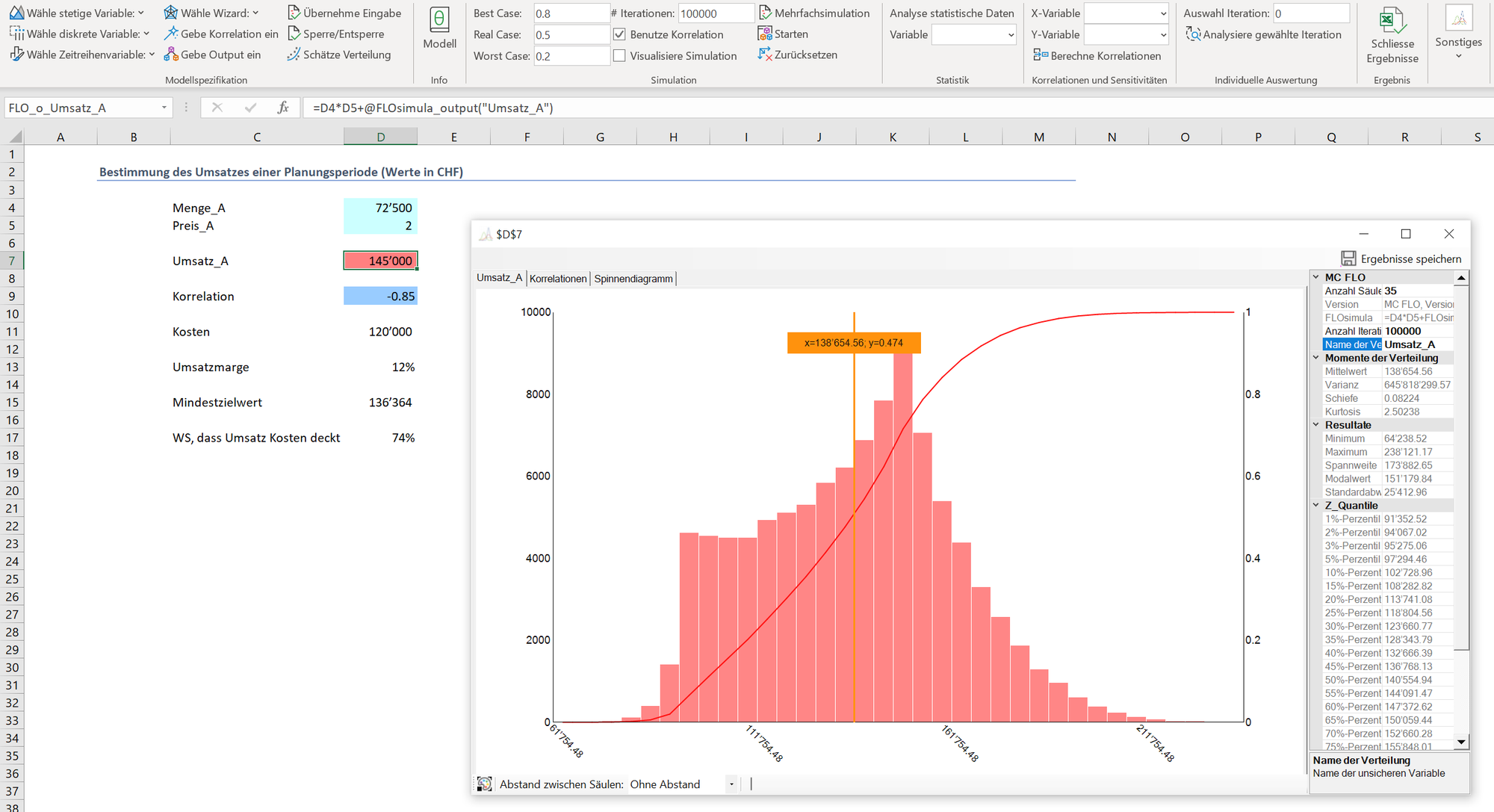
Eine Reflektion über die Multiplikation von zwei unsicheren Grössen (Preis, Menge) im Rahmen der Unternehmensplanung.
02. Dezember 2019
Der Zahlungsverzug kann ein Unternehmen schnell in Bedrängnis bringen, insbesondere dann, wenn Wahrscheinlichkeiten unsachgemäss herangezogen werden. Wir zeigen Ihnen, wie Sie mit einer Simulation die Unsicherheit in den Griff bekommen.
04. November 2019
In vielen Bereichen haben sich Simulationen durchgesetzt. Wir finden, dass selbst bei staatlich verordneten Preisen eine Simulation angebracht ist.
04. Oktober 2019
Monte-Carlo Simulationen sind in der Lage, die in der Zukunft herrschende Unsicherheit einzuzäunen und diese für die Planung nutzbar zu machen.