Auch wenn Monte-Carlo Simulationen ein hilfreiches Instrument darstellen, sind bei der Modellierung Stolpersteine aus dem Weg zu räumen. Ein Problemfall stellt in vielen Fällen die Multiplikation von zwei unsicheren Variablen dar. Warum, zeigen wir Ihnen hier.
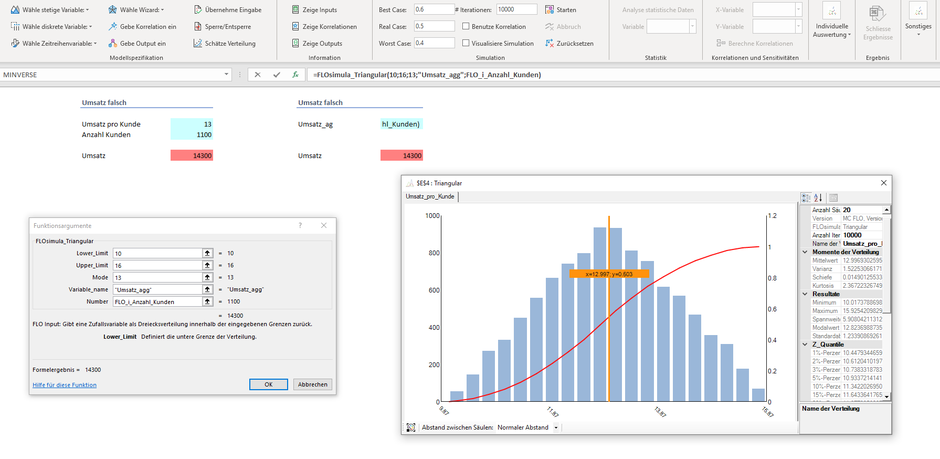
Stellen Sie sich vor, dass Sie vor der Aufgabe stehen, den Umsatz eines Produktes unter Unsicherheit anhand einer Simulationsrechnung auszuweisen. Dabei werden Ihnen der Umsatz pro Kunde und die Anzahl der Kunden, beide als unsichere Grössen, genannt.
In MC FLO kann dies wie folgt modelliert werden:
- =FLOsimula_Triangular(10;16;13;"Umsatz_Kunde")
- =FLOsimula_Uniforme(1000;1200;"Anzahl_Kunden")
- =FLO_i_Umsatz_Kunde*FLO_i_Anzahl_Kunden+FLOsimula_output("Umsatz_falsch")
Der Umsatz ergibt sich in diesem Fall als Produkt beider Grössen. Dabei ist der «Umsatz pro Kunde» als Dreiecksverteilung mit einem Minimum von CHF 10 und einem Maximum von CHF 16 und die «Anzahl Kunden» als Gleichverteilung mit den Grenzen 1'000 und 1'200 definiert. Aber warum haben wir dies als «Umsatz falsch» klassifiziert?
Stellen wir uns vor, dass bei der Iteration «n» die «Anzahl Kunden» mit 1'000 und der «Umsatz pro Kunde» mit CHF 10 angenommen wird. Die Multiplikation unterstellt, dass in diesem Fall genau alle 1'000 Kunden exakt CHF 10 Franken ausgeben. Dies ist aber extrem unrealistisch. Vielmehr müssten bei dieser Iteration 1'000 Kunden mit einem «Umsatz pro Kunde» zwischen 10 und 16 Franken angesetzt werden. Die Schwankungsbandbreite ist im letzten Fall über alle «n» Iterationen somit viel geringer als beim ersten Ansatz.
Mit der demnächst erscheinenden Version Sotelo haben wir MC FLO konsequent auf eine einfache Handhabung bei einer Multiplikation ausgerichtet. Neu können Sie in jeder beliebigen Verteilungsfunktion (stetig oder diskret) optional die Anzahl Vorkommnisse angeben. Bei jeder Iteration wird dann diese Anzahl mit der unbekannten Grösse (hier Umsatz pro Kunde) angesetzt. Als Folge erhalten Sie dann die Summe über alle Vorkommnisse.
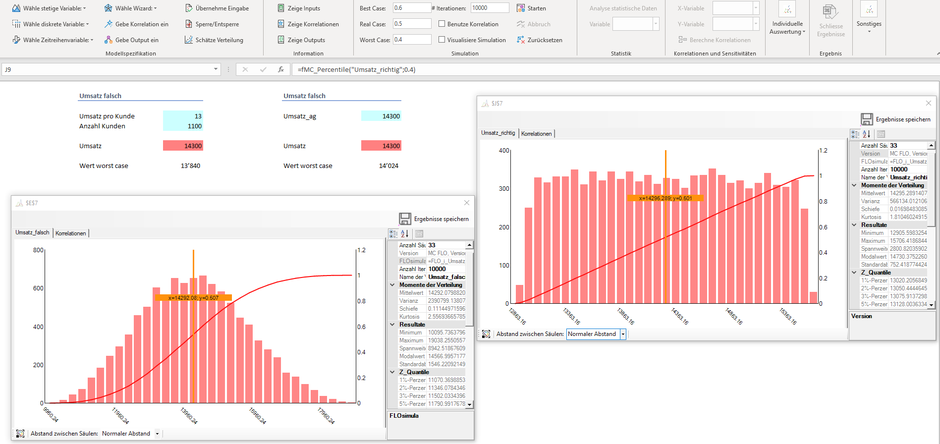
Schauen wir uns dies am Beispiel an: Unter «Umsatz falsch» wird ein Minimalwert von ca. TCHF 10 und Maximalwert von ca. TCHF 19 ausgewiesen. Unter «Umsatz richtig» betragen diese Werte TCHF 13 und TCHF 16. Bei beiden Ansätzen wird ein Mittelwert von ca. TCHF 14 ermittelt, hingegen ist die Abweichung um diesen Mittelwert im ersten Fall höher als beim zweiten, was bei der Risikomessung unangenehm auffällt.
Denn während der erste Ansatz im worst-case (hier als 40%-Quantil) einen Umsatz von ca. TCHF 13.9 ermittelt, beträgt dieser im zweiten Ansatz knapp TCHF 14. Zwar ist die Differenz hier gering, aber bei kritischen Quantilsgrenzen kann es zu immensen Unterschieden kommen, was anhand des Histogramms nachvollzogen werden kann.
Heisst dies nun, dass eine Multiplikation nur noch über den hier vorgestellten Ansatz umgesetzt oder gar auf diese verzichtet werden sollte? Mitnichten. Aber es kommt wie immer auf die Fragestellung an. Als Faustregel können Sie mitnehmen, dass Variablen, welche eine hohe Korrelation aufweisen (oder gar kausal zusammenhängen), über den traditionellen Ansatz multipliziert werden können. So etwa beim Produkt aus produzierter Menge und Stückkosten. Die Stückkosten ermitteln Sie ja, nachdem die produzierte Menge feststeht. Je höher die Menge, desto geringer die Stückkosten.
Umgekehrt, und hier mit einem anderen Beispiel ausgedrückt, wird der Schuhverkäufer nicht mit einem höheren Umsatz pro Kunde rechnen können, nur weil er 10 Kunden mehr bedienen darf.

Kommentar schreiben