La siguiente publicación de blog es más larga de lo habitual. Nuestra intención es combinar la planificación corporativa con la estadística generativa (bayesiana) y definir asimismo términos como "ambición" y "predicción" de una manera refrescante y nueva. Le sorprenderá que este tipo de proceso de planificación, que combina evaluaciones subjetivas con datos, se pueda configurar con Excel y MC FLO sin grandes inversiones en suites de planificación.
Para empresas la planificación significa, en el término más simple, amasar los procesos necesarios para crear los servicios/productos ofrecidos en el mercado, desde el flujo de ventas hasta los costes, con el objetivo de identificar los impulsores clave para el desempeño y remoldelarlas de tal forma que se maximice el valor de la empresa.
Cabe señalar que el futuro es incierto y las cifras a tener en cuenta durante el proceso de planificación estarán sujetas a fluctuaciones en torno al valor del plan inicial, que suele ser el valor medio esperado. Sin embargo, una empresa que tiene que dimensionar capacidades de producción, por ejemplo, no puede basarse únicamente en valores medios. Tiene que evaluar el espectro completo con sus probabilidades correspondientes para tomar las decisiones correctas. Además, se deben identificar desviaciones de los valores que se han tomado como objetivo (= ambición) y, usando nuevos conocimientos (datos), iniciar predicciones.
Para resolver todos estos problemas la estadística bayesiana en conjunto con el método Monte Carlo proporciona las herramientas necesarias.
Como costumbre y eludiendo fórmulas matemáticas, partimos de la siguiente situación: Una empresa recién fundada quiere proporcionar servicios de reparación de relojes en la región A. Como subtarea, la dirección tiene que preparar el plan de ventas para el primer año. Dado que hasta el momento no hay datos disponibles para la empresa, se deben utilizar estimaciones.
Supongamos que, teniendo en cuenta la experiencia previa de la gerencia en la industria relojera, una estimación fiable para el año (= 240 días hábiles) esté basada en lo siguentes números.
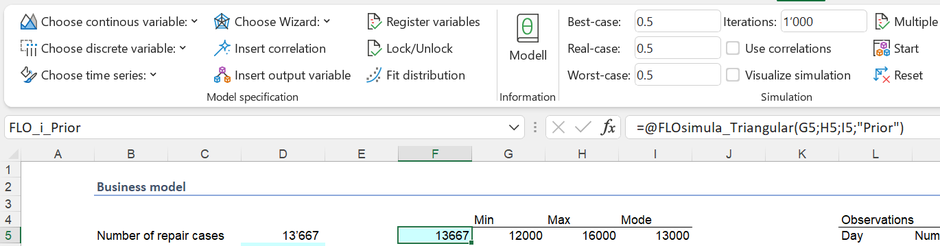
La gerencia asume que se ejecutarán un mínimo de 12.000 reparaciones facturables, un máximo de 16.000 y el valor más probable se estima en 13.000 unidades. Estas "estimaciones" se pueden reproducir usando distribuciones de probabilidad y, en el contexto de la estadística bayesiana, esta estimación representa nuestro conocimiento previo ("creencias", "a priori").
La configuración inicial del proceso de planificación requiere, en ausencia de datos, presunciones, que deben cuantificase. Esto distingue la estadística bayesiana moderna de la estadística frecuentista, donde las inferencias se obtienen utilizando experimentos aleatorios repetidos en condiciones comparables, y no sobre la base de suposiciones preliminares. Además, cabe también subrayarlo, el pensamiento bayesiano asume que los valores son intrínsecamente inciertos y, en consecuencia, declaraciones precisas como “la probabilidad de reelección de Joe Biden es exactamente el 30%” como tal ilusorias. Más bien, se asume un grado de creencia creíble. Una declaración relacionada podría ser: "Tengo un 95% de confianza que la posibilidad de reelección de Joe Biden en las próximas elecciones presidenciales está entre el 20% y el 40%". El enfoque en el "Yo" enfatiza que evaluaciones subjetivas ("conocimiento previo") se incorporan explícitamente en las estadística bayesiana (existe una descripción llamada bayesiana objetiva, sin embargo, el conocimiento pleno surge del enfoque subjetivo). El conocimiento previo se actualiza a través de datos (“evidencias”), de modo que se puedan realizar nuevas declaraciones a partir de éstas.
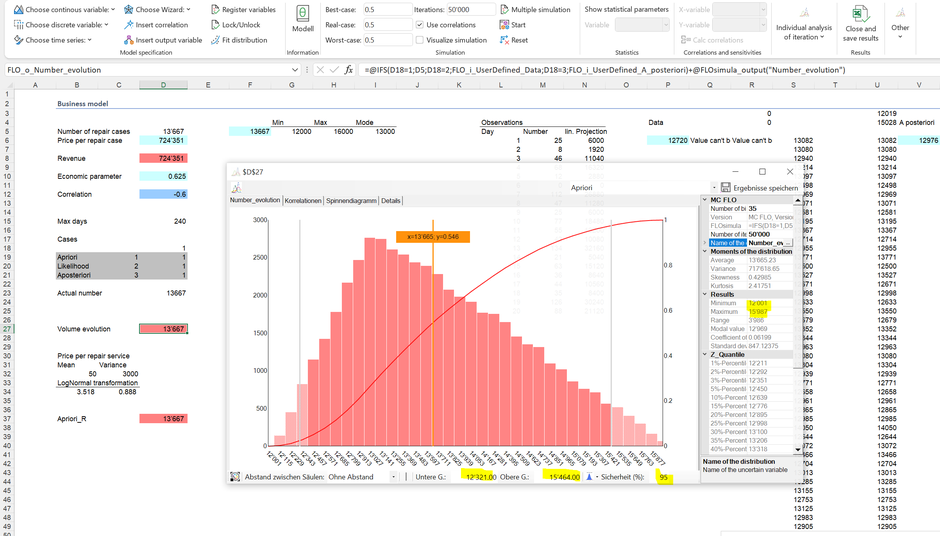
En relación con el número de reparaciones, que se derivó mediante una distribución triangular, se pueden derivar las siguientes conclusiones partiendo de una simulación (se han usado 50.000 iteraciones):
Se calcula un mínimo de 12.001 y un máximo de 15.987 pedidos de reparación, por lo que los valores no se desvían significativamente del mínimo y máximo teórico. El 95% de los resultados se encuentran entre 12.321 y 15.464 unidades, lo cual representa una predicción. Las fluctuaciones entre el mínimo y el máximo representan la incertidumbre. Los valores bajos pueden considerarse parte de un escenario pesimista, una alta demanda de pedidos sin embargo formará con alta probabilidad parte de un escenario optimista.
Como ya se subrayó anteriormente, una declaración de que el número de reparaciones durante el siguiente año será exactamente 13.000 (para poner un ejemplo) no es compatible con el concepto de probabilidad bayesiana. O para decirlo de otra manera: si admite solo un valor será preciso, pero no muy exacto.
Se puede utilizar el mismo procedimiento descrito anteriormente para derivar los precios de reparación. Un simple cambio de pila tiene un precio diferente al de una revisión de un reloj con tourbillon. Suponemos que el flujo de precios puede aproximarse mediante una distribución logarítmica normal, es decir, también analíticamente (ver columna B30ff). Sin embargo, nada impide a la gerencia de utilizar una función definida a través de un histograma o simplemente usando datos. Este es el quid de las estadística bayesiana: no existe un "verdadero" o "falso", sino un "bien fundamentado" y un "menos fundamentado". Las presunciones "menos buenas" se pueden ajustar en función de los datos disponibles (más sobre esto más adelante)*.
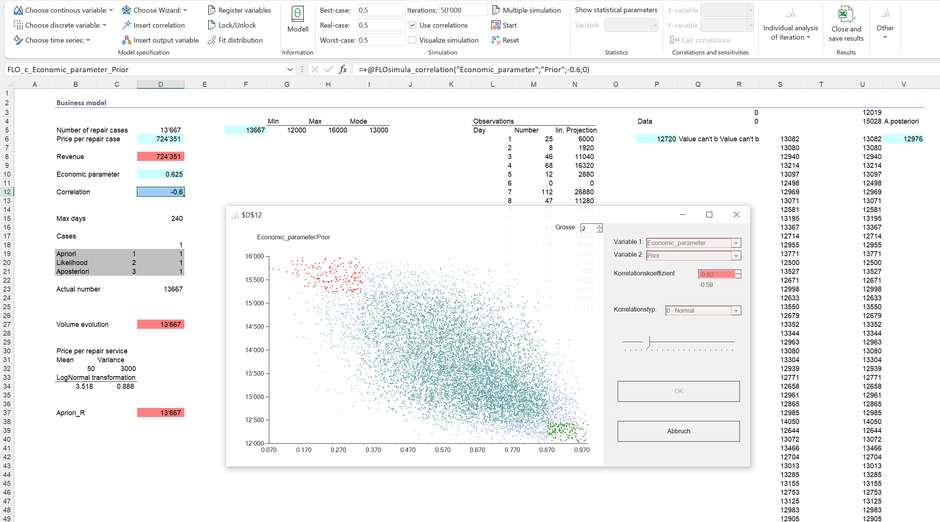
Un plan empresarial sólido cubre todos los impulsores relevantes. O para decirlo de otra manera: un modelo y, por tanto, el valor informativo de un plan depende de informaciones coherentes. Supongamos finalmente que el número de pedidos de reparación depende de las expectativas de la situación económica: si la economía está creciendo, es más probable que los consumidores compren relojes nuevos en lugar de reparar los existentes y viceversa. Esta dependencia se puede establecer numéricamente usando el concepto de la correlación, que se muestra en la celda D12.
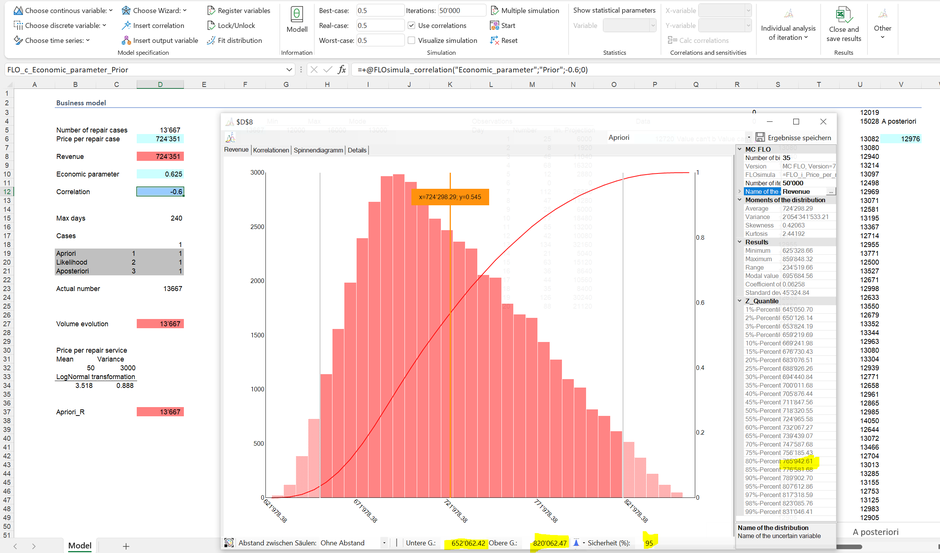
Como indicador de impulsor relevante, la gerencia está interesada en el flujo de los ingresos. Usando el concepto de la convolución, el producto de ambas variables (cantidad, precio) produce la distribución de ingresos a partir de la cual se pueden derivar más predicciones, haciendo hincapié en nuestras estimaciones a-priori:
Así vemos que el 95% de los resultados están entre 0,65 MCHF y 0,82 MCHF. De forma análogica a lo dicho anteriormente, podemos hacer la siguiente afirmación: "Basándonos en nuestras creencias, podemos tener un 95% de certeza de que los ingresos dentro de un año oscilarán entre 0,65 MCHF y 0,82 CHF". De tal declaración se puede derivar la "ambición". Si la gerencia establece un objetivo de ingresos de 0,5 MCHF, la probabilidad de superar este objetivo sería del 100% y, por lo tanto, no sería ambicioso (el mínimo simulado de aproximadamente 0,62 MCHF está por encima de este objetivo de ventas). Por otro lado, un objetivo de ingresos de 1 MCHF sería ambicioso, pero no alcanzable.
Una ambición del 20% (es decir, el 80% de los resultados están por debajo de este valor) equivale a un objetivo de ventas de al menos 766.000 CHF. Este objetivo se puede lograr, pero solo con una probabilidad del 20%. Es tarea clave de la gerencia definir el nivel de ambición específico de antemano o cuando los primeros datos estén disponibles.
Supongamos que la dirección ha fijado una ambición del 30% y, por tanto, espera un objetivo de ventas de aprox. 748.000 CHF.
El proceso de planificación, que define la interacción de los impulsores relevantes y que se cierra con el establecimiento de objetivos, se ha completado en nuestro caso (la realidad es naturalmente más compleja [comportamiento de los competidores, etc.]). Si surgieran nuevos impulsores, por ejemplo, debido a un modelo comercial ampliado, el modelo tendría que ser adaptado. Este proceso de actualización del modelo debe separarse de la cuestión de cuándo y cómo actualizar los parámetros para medir el alcanze de nuestros objetivos.
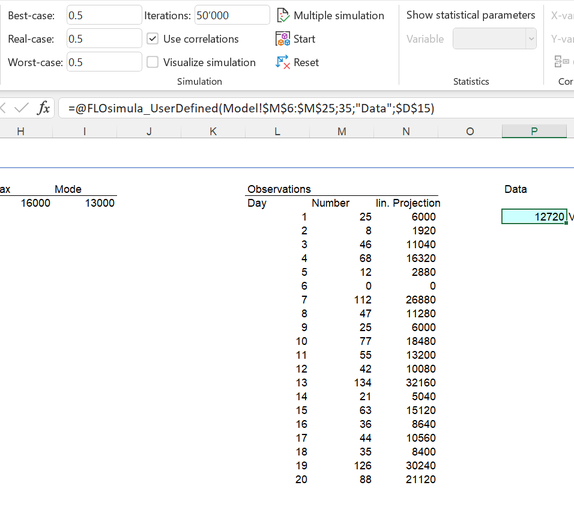
Después de un mes (= 20 días hábiles), los primeros datos de los pedidos de reparación facturables están disponibles:
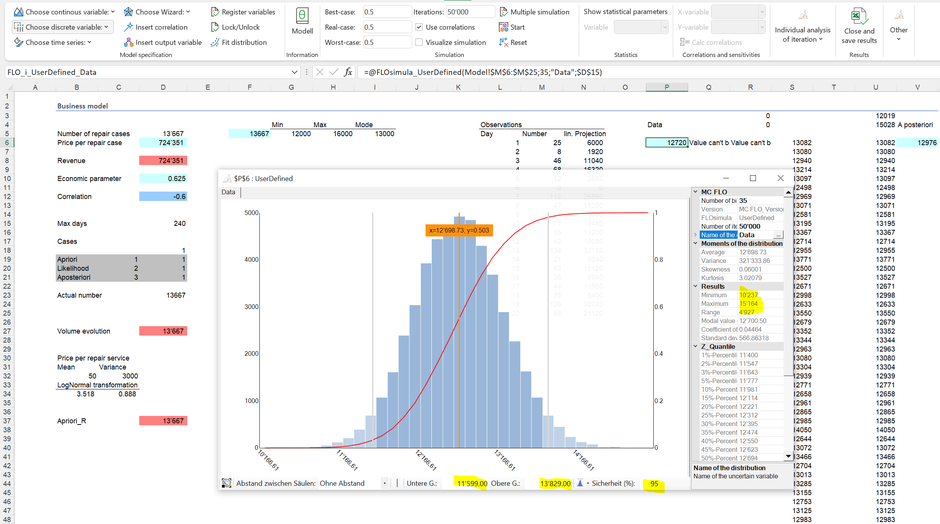
No se llevaron a cabo órdenes de reparación el día 6; sin embargo, el mayor número de pedidos de reparación en un día es 134 (día 13). La estadística bayesiana nos permite combinar los datos (“evidencia”) con nuestro conocimiento previo para derivar un conocimiento actualizado (a-posteriori). Para hacer esto, lo primero que debe hacerse es determinar la función de probabilidad (o verosimiltud) a partir de los datos (likelihood). Eso suena muy técnico, pero es relativamente fácil de implementar para la mayoría de las tareas de planificación. La idea es la siguiente: dado que solo tenemos estos datos y con éstos tendríamos que hacer una predicción para un año, ¿cómo procederíamos? La forma ingenua, y desafortunadamente incorrecta, es extrapolar las observaciones individuales linealmente al año. Si tenemos 25 órdenes de reparación por día, una extrapolación lineal muestra que después de un año se han realizado un total de 6.000 (25 * 240) reparaciones. Sin embargo, la probabilidad de que se produzcan exactamente 25 órdenes de reparación por día durante 240 días consecutivos es muy baja. En los datos disponibles de 20 días, solo pudimos observar dos veces 25 órdenes de reparación. Por lo tanto, buscamos combinaciones que maximicen los valores observables probables. Esta es entonces nuestra verosimiltud o likelihood. Esto puede iniciarse usando la técnica de convolución y completarse usando una simulación de Monte Carlo. MC FLO lo apoya con la posibilidad de vincular el número relevante (aquí 240 días hábiles) directamente con los datos (ver columna P). Aquí está la función de verosimilitud correspondiente después de 50.000 iteraciones-
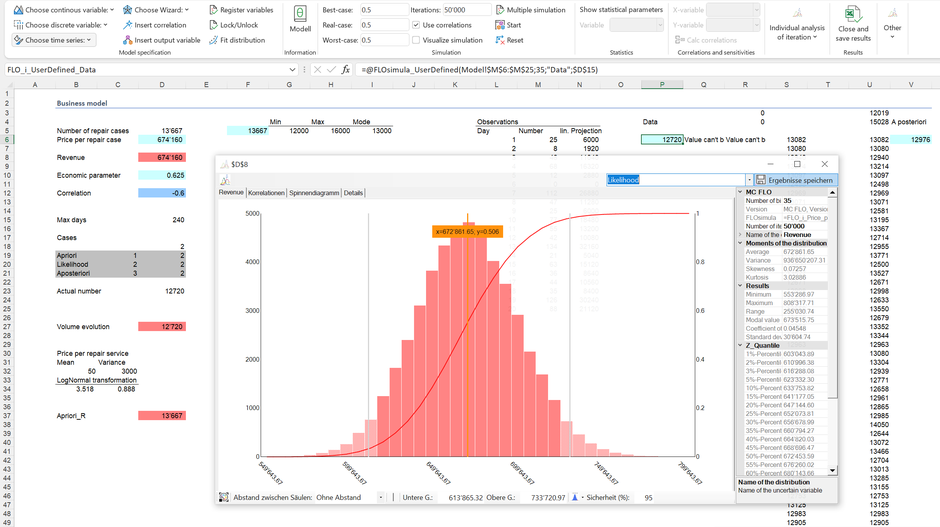
La función de verosimiltud muestra que el número de reparaciones basado en los datos tiende a variar entre 10,237 y 15,164 unidades en un año. En combinación con la función de precios se dará como resultado la siguiente distribución para los ingresos (por motivos de simplicidad asumimos que la evidencia sobre los precios y la correlación es igual a nuestro conocimiento previo):
Come se puede ver, el 95% de los resultados se encuentran entre 0,61 MCHF y 0,73 MCHF; el máximo apena sobrepasa 0,81 MCHF.
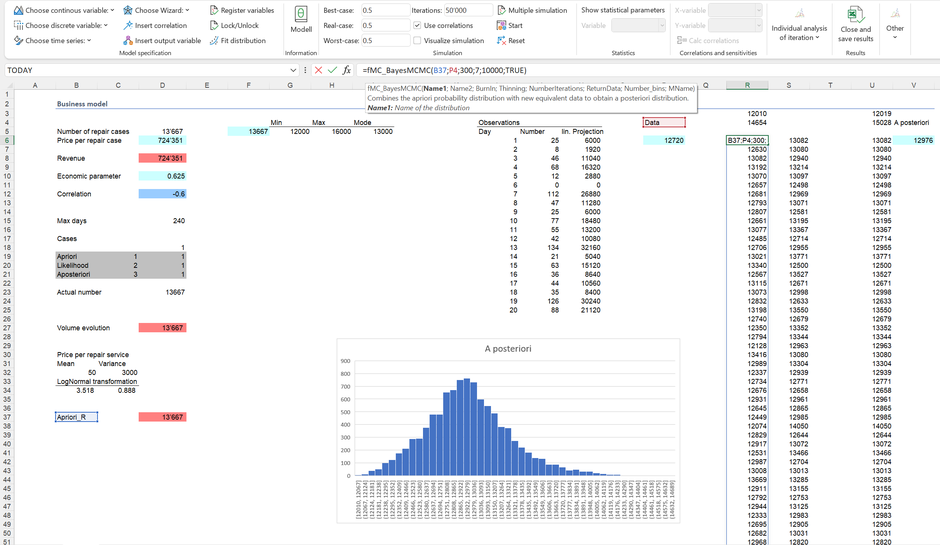
El siguiente paso es combinar la verosimiltud (likelihood) con nuestro conocimiento previo. Con la fórmula correspondiente de MC FLO "fMC_BayesMCMC", se hace una muestra a partir de la denominada distribución "a posteriori", es decir, el resultado de la combinación de la verosimiltud con el conocimiento previo. Los correspondientes datos se almacenan como una función definida por el usuario. Al igual que el conocimiento previo, esta distribución a-posteriori sirve para iniciar predicciones **.
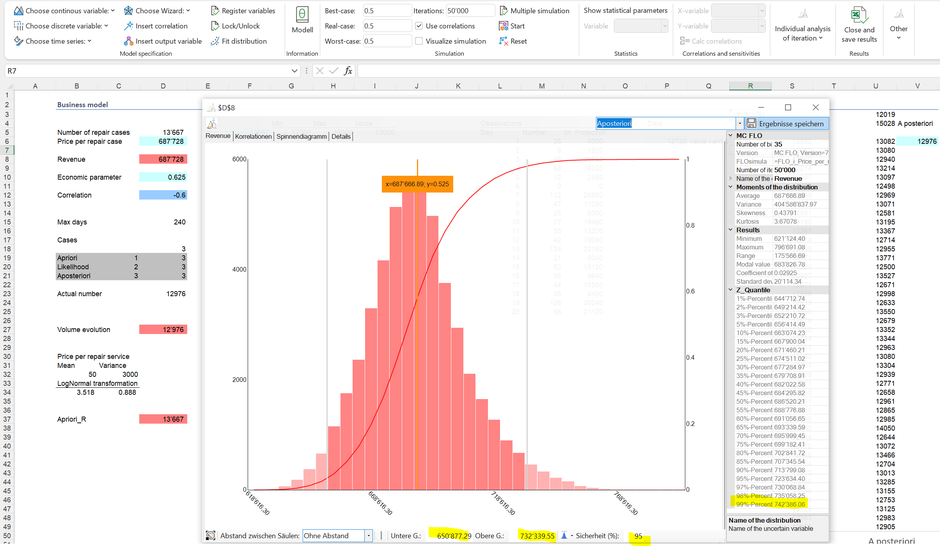
Después de una nueva simulación, en la que el conocimiento previo en la celda D5 fue sustituido por la distribución a posteriori, se muestra el siguiente resultado (asumimos que los resultados del primer mes están completamente contenidos en la distribución a posteriori):
En el 95% de los casos la facturación estará entre 0,65 y 0,73 MCHF. Por el contrario, la probabilidad de que las ventas superen el objetivo de 0,77 MCHF es ahora inferior al 1%.
La gerencia utiliza los datos observados y la distribución a-posteriori para decidir si mantener la ambición previamente definida o si debería ajustarlos en función de los datos (incluso puede ajustar su conocimiento previo [los datos no son de todo compatibles con las presunciones a-priori]). La gerencia puede esperar otro mes y luego usar los nuevos datos para combinarlos con el “conocimiento previo” (nuestra distribución a-posteriori calculada) para obtener una nueva distribución a-posteriori actualizada. Sin embargo, si se mantiene la ambición original, se deben definir las medidas que contribuyan a un aumento de las ventas. Dado que no puede influir en los factores externos, como en la expectación de la situación económica, la configuración de nuestro modelo solo permite ajustar los precios para alcanzar los objetivos.
Conclusión: la estadística bayesiana junto con el método Monte Carlo se puede utilizar de forma eficaz para la planificación empresarial. Se basa en el concepto del conocimiento previo (a-priori), que cuantifica valoraciones subjetivas y permite actualizar este conocimiento previo a partir de nuevos datos.
* Los estudios de riesgo muestran que las personas están expuestas a sesgos en la recopilación de conocimientos previos (por ejemplo, al evaluar probabilidades incorrectamente). Esto es cierto, pero en la medida en que usamos datos para actualizar nuestro conocimiento, estos sesgos se diluyen con el paso del tiempo.
** Mucha gente piensa que solo deberíamos confiar en los datos, en este caso en la verosimiltud (likelihood). Pero esto claramente debe ser negado desde una perspectiva bayesiana. ¿Qué pasa si los datos disponibles aún no reflejan toda la verdad? Esta es exactamente la razón por la que nuestro conocimiento previo es importante. Con el transcurso del tiempo, los datos, si el conocimiento previo no fue clasificado como «absoluto», dominarán.
Anécdota: La estadística moderna desarrollada por el reverente Thomas Bayes independientemente de Laplace se hico pública después de su muerte. Una presunción es que Bayes rechazó una publicación porque la transición de conocimiento previo usando datos al conocimiento adaptado (a-posteriori) contradice la creencia incondicional en Dios. La famosa fórmula bayesiana solo tiene sentido si el conocimiento previo no se declara como absoluto, de lo contrario, incluso los mejores datos no pueden conducir a un conocimiento adaptado. En otras palabras: Hay que dudar de Dios para que el conocimiento previo se pueda convertir en un conocimiento a-posteriori adaptado.
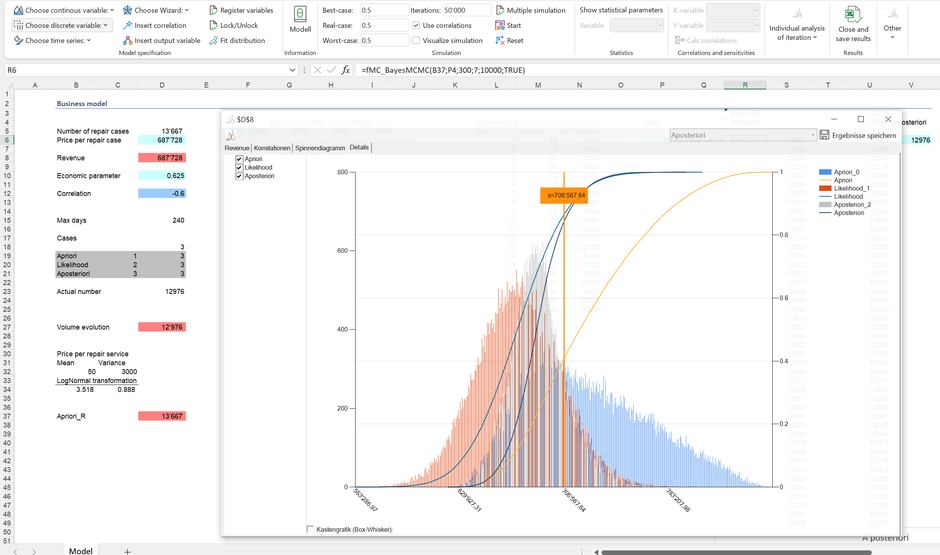
El gráfico ayuda a explicar la determinación de la distribución a posteriori utilizando el algoritmo de Metropolis-Hasting incorporado en MC FLO: Para valores que están contenidos tanto en nuestro conocimiento anterior (a-priori) como en la verosimiltud, existe una alta probabilidad de que se incluyan en la distribución a posteriori; por otro lado, la probabilidad de admisión disminuye si los valores difieren y están muy alejados.
Las funciones presentadas y el libro de trabajo de Excel correspondiente están disponibles en MC FLO a partir del versión 7.6 y superior.
Esta publicación de blog se ha utilizado con la localización en alemán habilitada en Microsoft Excel.

Kommentar schreiben