Von 200 Münzwürfen wurden 114 mal die Kopf, 86 mal folglich Zahl gemessen. Ist das Ergebnis auf die Benutzung einer fairen Münze zurückzuführen oder ist die Münze manipuliert worden? Auf Basis einer Stichprobe (hier 200 Münzwürfe) sollen allgemeine Aussage getroffen werden, um so bessere Entscheidungen (etwa Wettstrategie) zu treffen. Das ist Statistik.

Die Bayessche Statistik geht – analog der klassischen Statistik – davon aus, dass die Daten (hier die 200 Münzwürfe) aus einem datengenerierenden Prozess (DGP) entstammen, dieser Prozess oftmals als Modell mit einer oder mehreren Zufallsvariablen ausgedrückt werden kann und die dafür verwendeten Parameter konstant sind. Während die klassische Statistik die Parameter eines Modells als einen Punktwert ausgibt und die Unsicherheit über den wahren Wert mittels Nebenrechnungen ausgedrückt wird, geht die Bayessche Statistik von vorne herein davon aus, dass der gesuchte Wert als unsicher zu betrachten und somit als Wahrscheinlichkeitsverteilung darzustellen ist. Das erlaubt auch ganz andere Möglichkeiten Modelle oder gar Hypothesen miteinander zu vergleichen (die klassische Statistik kann hingegen nur eine Hypothese stützen oder verwerfen aber nicht eine Hypothese gegenüber die Alternativhypothese bewerten).  

Zu unserem Beispiel: Wird davon ausgegangen, dass das Werfen einer Münze einer Bernoulli-Verteilung folgt (mit Ausgang 1 (= Kopf) oder 0 (= Zahl)) und jeder Wurf unabhängig ist, kann der datengenerierende Prozess von 200 Würfen als Binomialmodell dargestellt werden. Der entscheidende Paramater und somit gesuchte Wert einer Binomialverteilung ist die Wahrscheinlichkeit, mit der ein Ereignis (hier der Bernoulli-Prozess) den Wert 1 (= Kopf) annimmt. Würde ein erneutes Spiel mit 200 Münzwürfen durchgeführt werden, würde trotz eines datengenerierenden Prozess anhand eines Binomialmodells mit dem Parameterwert von 0,5 ein anderer Wert für die Anzahl Kopf als die gemessenen 114 resultieren. Dies ist als Stichprobenvariabilität bekannt. 

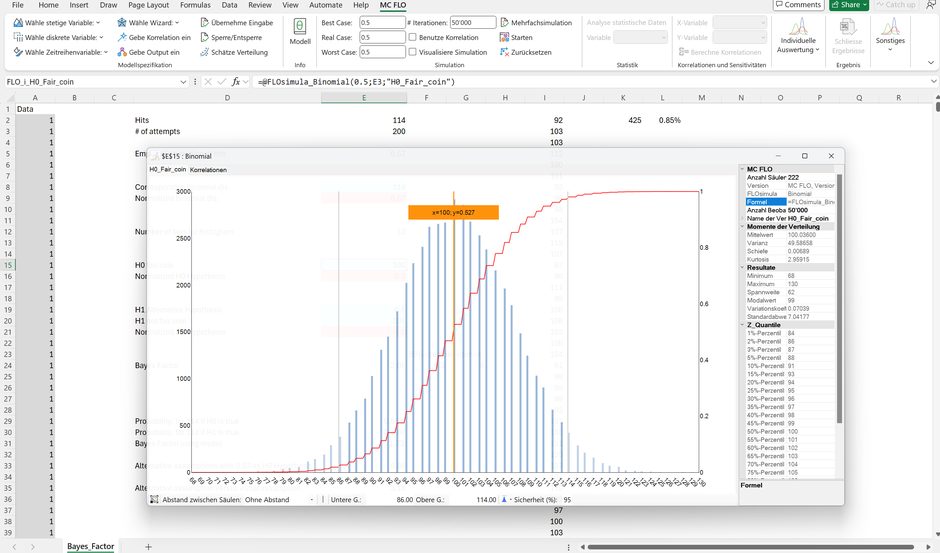
Abbildung: Resultat einer Simulation eines DGP von 200 Münzwürfen anhand Binomialmodell mit Kopf-Trefferwahrscheinlichkeit von 50% (Nullhypothese). Im Erwartungswert haben 100 Münzen das Resultat «Kopf». 

Die Frage lautet: Ist die beobachtete Anzahl von 114 Kopf mit der Nullhypothese, der Parameter des Binomialmodells beträgt 0,5 vereinbar oder ist die Alternativhypothese, der Parameter nimmt einen Wert ungleich 0,5 an, anzunehmen? 

Der Bayes-Faktor baut auf den Satz von Bayes auf, wobei die Likelihood und die Vorabwahrscheinlichkeit im Vordergrund stehen. MC FLO geht davon aus, dass die Vorabwahrscheinlichkeit für die Nullhypothese und die Alternativhypothese jeweils 50% beträgt, somit das Ergebnis nicht beeinflussen. Entscheidend ist somit die Likelihood. 

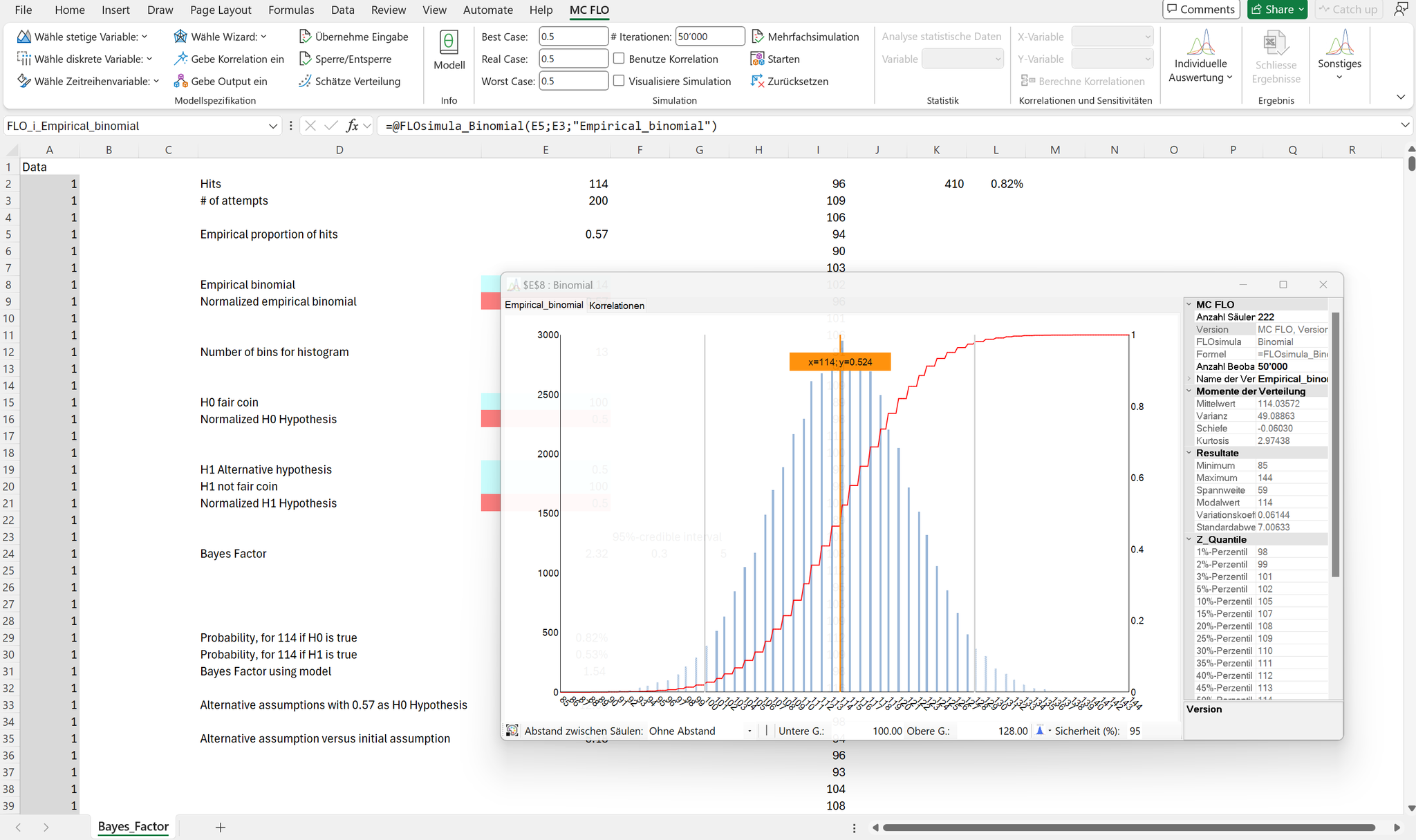
Die Likelihood nimmt die gemessene Anzahl von Münzwürfen und die resultierende Kopfergebnisse von 114 als gegeben an und variiert den Parameter des Binomialmodells. Würde der wahre Parameter ca. 0,57 entsprechen, wären wir beim «Maximum Likelihood» Schätzer, d.h. bei einem Parameter von 0,57 wäre der gemessene Wert von 114 Kopfergebnissen am ehesten zu erwarten. 

Die Bilder spiegeln das Ergebnis der Likelihood der 114 gemessenen Ergebnisse «Kopf» bei 200 Münzwürfen und die möglichen Ergebnisse bei Variation des Parameters.

Ein Parameterwert von 0,5 ist hingegen mit dem gemessenen Wert von 114 Kopfergebnissen für sich allein betrachtet hingegen weniger wahrscheinlich (die Wahrscheinlichkeit ein Kopfergebnis von mindestens 114 oder höher zu beobachten, beträgt nur ca. 2,5%, «p-Wert»). Die klassische Statistik würde bei einem zweiseitigen Hypothesentest zur Schlussfolgerung kommen, dass die Nullhypothese zu verwerfen und die Alternativhypothese anzunehmen ist. 

Zwei Bemerkungen für die Einordnung des Bayes-Faktor seien vorangestellt: 1. Die klassische Statistik untersucht die Alternativhypothese nicht dezidiert, sondern nimmt automatisch durch Verwerfung der Nullhypothese diese an. 2. Die klassische Statistik bindet Aussagen zu nicht beobachteten Werten in die Entscheidungsfindung ein (hier Kopfergebnisse grösser als 114, obwohl in der Stichprobe effektiv nur 114 gemessen wurden), der Bayes-Faktor berücksichtigt hingegen nur die gemessenen Zahlen. 

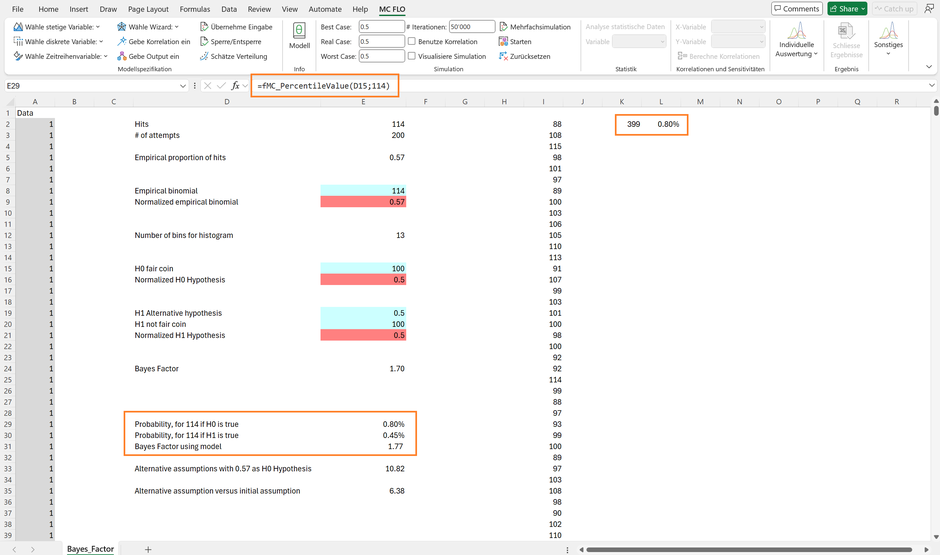
Der Bayes Faktor entspricht dem Verhältnis der Likelihood aus der Nullhypothese und der Likelihood aus der Alternativhypothese. In Bezug auf die Nullhypothese ist anhand des unterstellten Binomialmodells die Wahrscheinlichkeit zu ermitteln, ein Kopfergebnis von 114 zu erhalten, gegeben dass der Parameterwert 0,5 beträgt.

Von 50'000 durchgeführten Simulationen sind 399 Beobachtungen mit 114 Kopfergebnisse bei jeweils 200 Münzwürfen gezählt worden, die Wahrscheinlichkeit beträgt somit 0.80% (399 / 50'000).

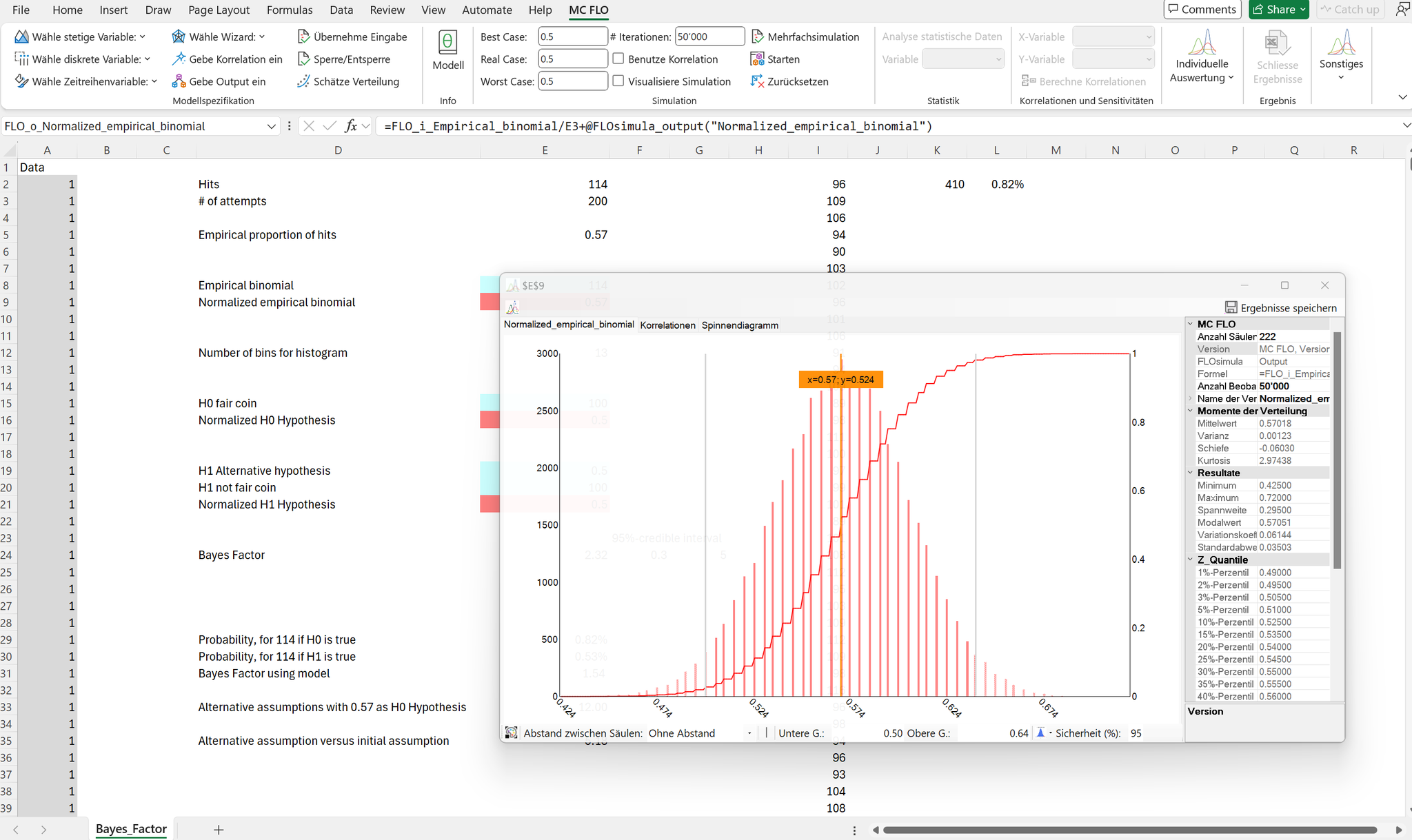
Die Alternativhypothese geht davon aus, dass der DGP anhand eines Binomialmodells mit irgendeinem Parameterwert zwischen 0 und 1 Gültigkeit hat. Zur Beschreibung dieses angepassten DGP kann das Beta-Binomialmodell beigezogen werden. Hierbei wird das Binomialmodell jeweils mit einem zufälligen Wert zwischen 0 und 1 angesetzt und das Resultat hiervon als Beobachtung aufgenommen. Die resultierende Verteilung entspricht einer Gleichverteilung mit dem Minimum von 0 (= Parameterwert entspricht 0, somit Kopfergebnis ebenfalls gleich 0) und einem Maximum von 200 (= Parameterwert entspricht 1, somit Kopfergebnis gleich Anzahl Münzwürfe).

Beta-Binomialmodell mit Parameterwert zwischen 0 und 1; 200 Münzwürfe. 

Die Wahrscheinlichkeit auf dem Beta-Binomialmodell ein Ergebnis von 114 zu erzielen, beträgt nur 0,45%. Der Bayes Faktor entspricht somit 0,80% / 0,45% = 1,77. Die Nullhypothese ist somit um den Faktor 1,77 gegenüber der Alternativhypothese vorzuziehen. Ob anhand eines Faktor von 1,5 oder 10 die Nullhypothese mit glaubwürdiger Sicherheit vorzuziehen ist, bleibt eine Sache des Ermessens. Praktiker geht oft davon aus, dass – analog dem Signifikanzwert in der klassischen Statistik - ein Bayes-Faktor von über 3 die Nullhypothese bestätigt.  

Der Bayes-Faktor kann nun aber auch zum Vergleich konkurrierender Ansichten beigezogen werden. Nehmen wir an, dass Sofia im Gegensatz zu Peter von der Annahme ausgeht, dass der wahre Parameterwert 0,57 statt 0,5 beträgt. Analog oben können wir auch hier den Bayes-Faktor ermitteln, welcher 10,82 beträgt. Wie gut ist die Modellannahme von Sofia gegenüber der Ausgangsannahme von Peter, dass der Parameter 0.5 beträgt? Hierzu setzen wir beide Bayes-Faktoren ins Verhältnis; 10,82 / 1,77 = 6,38. Der Bayes-Faktor von 6,38 liegt über den «kritischen» Wert von 3 und würde die Annahme von Sofía bestätigen.

Anstatt über den bisher beschriebenen Weg zur Entscheidungsfindung zu kommen, können Sie mittels der Formel «fmc_BayesFactor» die Berechnung direkt ausführen. Hierzu geben Sie die theoretische Aufteilung («Nullhypothese») als erstes ein (hier 0,5), gefolgt von der ermittelten, empirischen Aufteilung (hier 0,57 = 114 Kopf / 200 Münzwürfen) und der Anzahl Versuche (hier 200 Münzwürfe). MC FLO errechnet dann anhand 50'000 möglicher Werte des Binomialmodells und des Beta-Binomialmodells den Bayes Faktor aus; hier den Wert von 1,70. 

Dieser Wert ist nicht mit dem bisher ermittelten Wert von 1,77 identisch, was auf die Stichprobenvariabilität zurückzuführen ist. Sie können die Anzahl Iterationen, Versuche und jeweilige Schranken zur Ermittlung eines glaubwürdigen Intervalls des Bayes-Faktors optional eingeben. Beachten Sie aber, dass die Ermittlung des glaubwürdigen Intervalls je nach Spezifikation ca. 1'000 Versuche benötigt. Bei angenommen 50'000 Iterationen je Versuch wären somit 50 Mio. Berechnungsschritte für jedes Modell (somit 100 Mio. Berechnungsschritte für Null – und Alternativhypothese) nötig, was die Berechnungsdauer in Microsoft Excel markant erhöht.    

Fazit: Der Bayes-Faktor erlaubt den direkten Vergleich von konkurrierenden Modellen / Annahmen. Sie können damit in der Praxis immer wiederkehrende Fragestellungen auf eine angenehme frische, intuitive aber auch wissenschaftlich fundierte Methode antworten.