Mit den Funktionen fMC_NBT (Newcomb-Benford-Test) und fMC_LDT (Last-Digit-Test) können Sie Daten auf bestimmte Muster testen. 

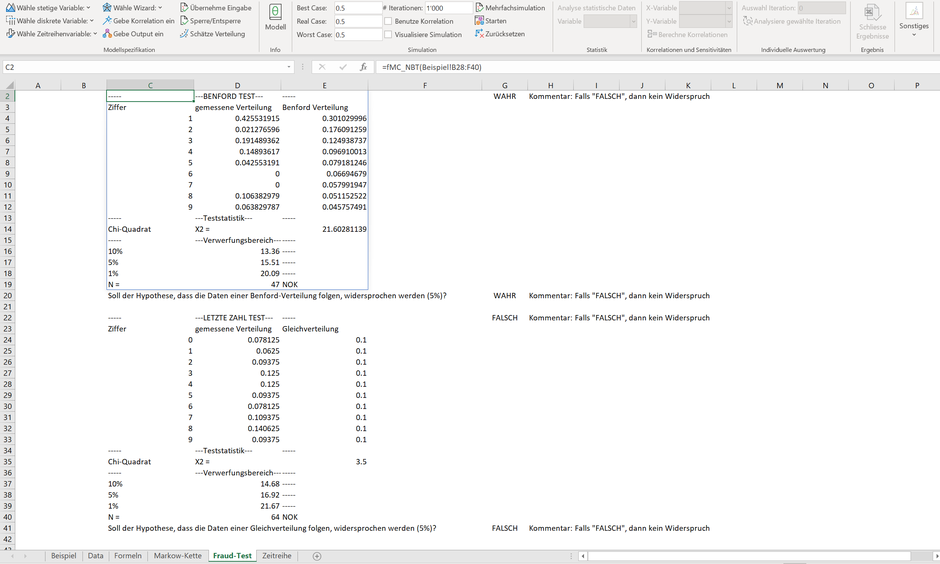
Der Newcomb-Benford-Test (NBT) überprüft, ob die erste führende (von 0 verschiedene) Zahl einer Benford Verteilung folgt. Bei der Benford Verteilung wird unterstellt, dass Zahlen beginnend mit "1" ca. 30% der untersuchten Zahlen ausmachen und nur ca. 4.5% aller Zahlen mit einer "9" beginnen (siehe Zelle E4ff. im unten aufgeführten Beispiel). Es wird vermutet, dass Zahlen aus der Buchhaltung (etwa Tagesumsätze) einer solchen Verteilung folgen. Mit einem Test können Sie überprüfen, ob dies für die untersuchten Zahlen der Fall ist. 

Der Last-Digit-Test (LDT) überprüft, ob (von 0 verschiedene) Zahlen vor dem Gleitkommazeichen einer Gleichverteilung folgen. So wird unterstellt, dass die "0" als letzte Zahl ca. 10% der untersuchten Zahlen ausmachen, wie auch die Zahlen "1" bis "9" (siehe Zelle E24ff.). Mit einem Test können Sie prüfen, ob dies für die untersuchten Zahlen der Fall ist. 

In beiden Fällen wird der chi-2 (Chi-Quadrat) Test herangezogen. Sowohl die Testprüfgrösse ("X2") als auch dezidierte Verwerfungsbereiche werden als Resultat ausgegeben. Anhand des Verwerfungsbereich legen Sie fest, ob Sie die Nullhypothese ("Daten folgen der unterstellten Verteilung") verwerfen sollen oder nicht. Liegt die Testprüfgrösse über den Verwerfungsbereich, dann sollten Sie die Nullhypothese ablehnen und stattdessen die Alternativhypothese ("Daten folgen nicht der unterstellten Verteilung") annehmen. Beachten Sie aber bitte, dass ein Test kein mathematischer Beweis ist. 

Info: Sollte die Anzahl der untersuchten Zahlen geringer als 51 (NBT) oder geringer als 61 (LDT) oder die Anzahl je Bereich geringer als 5 sein, wird ein "NOK" neben der Anzahl der untersuchten Daten ("N=") ausgegeben. Beachten Sie bitte, dass der chi-2 Test sehr sensitiv auf Ausreisser reagiert. Mit steigender Anzahl der untersuchten Daten ("N") führen bereits wenige Ausreisser zur Ablehnung der Nullhypothese, obwohl dies nicht begründet erscheint. Sie sollten im Zweifel dann auf andere Test-Verfahren und Instrumente zurückgreifen.  

Achten Sie darauf, dass die untersuchten Zellen keine Excel-Fehler (wie #Wert!, #Div/0!) enthalten, andernfalls werden die damit verbundenen Fehlercodes als Zahl interpretiert und bei der Bewertung herangezogen. 

Beachten Sie zudem, dass MC FLO beim Last-Digit-Test bei ganzen Zahlen die letzte Zahl heranzieht (für die Zahl "1234" wird somit die "4" als Last-Digit verwendet). 

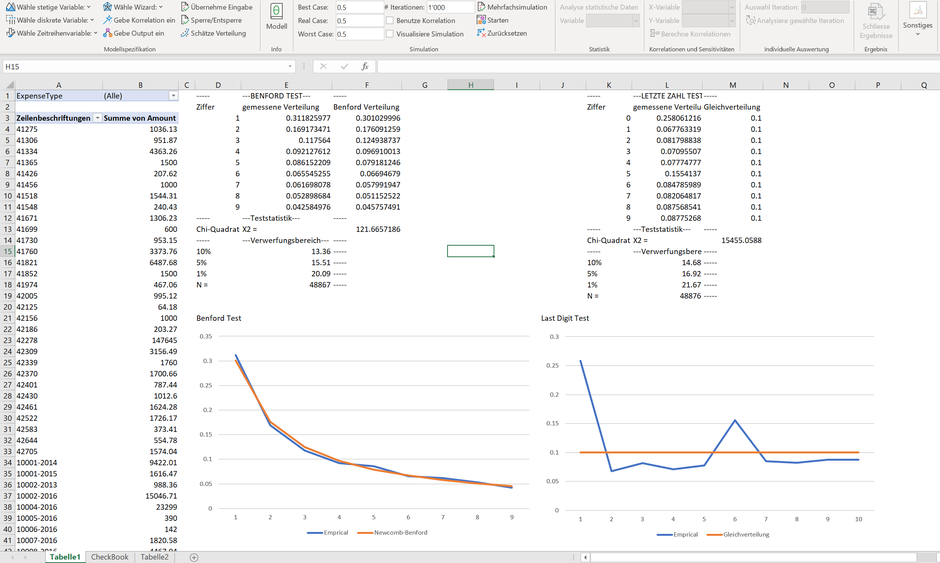
Vorliegend werden Daten aus der Buchhaltung einer fiktiven Organisation untersucht. Für den NBT-Test wird ein X2 von 121.66 (Zelle F13) bei 48'867 gültig geprüften Zahlen ausgegeben; X2 liegt sowohl über den Verwerfungsbereich von 10% mit 13.26 als auch über den Verwerfungsbereich von 1% mit 20.09 einer chi-2 Verteilung mit 8 Freiheitsgraden.

Um die Nullhypothese aufrecht zu erhalten, müsste der Wert von X2 geringer als der maximal mögliche einer chi-2 Verteilung mit 8 Freiheitsgraden (die Zahl der Freiheitsgrade ergibt sich aus der untersuchten Anzahl möglicher Ausprägungen, hier 9, wovon 1 subtrahiert wird) ausfallen. 

Wie aus der Simulation einer chi-2 Verteilung ersichtlich, liegt das Maximum bei 8 Freiheitsgraden bei ca. 43.94 (siehe "Maximum"  unter "Resultate") und somit deutlich unter dem errechneten X2 von 121.66. Oder anders: der Wert von 121.66 kann nicht aus einer chi-2 Verteilung mit 8 Freiheitsgraden entstammen. Die Nullhypothese, wonach die untersuchten Zahlen einer Benford-Verteilung folgen, ist somit zu verwerfen. 

P.S: Läge der X2 hingegen bei ca. 15.5, würde bei einem Signifikanzniveau von 5% (oder auch Verwerfungsbereich) die Nullhypothese nicht verworfen. Sprich: bei einem X2 von 15.5 liegen 95% aller möglichen Werte einer chi-2 Verteilung mit 8 Freiheitsgraden links von 15.5, 5% rechts davon. 

Die Interpretation des LDT ist analog des NBT, mit dem Unterschied, dass hier eine chi-2 Verteilung mit 9 Freiheitsgraden heranzuziehen ist.