Nach Durchführung einer Simulation werden neben der resultierenden Verteilung auch Kennzahlen, sowohl graphisch als auch numerisch, ausgegeben. 

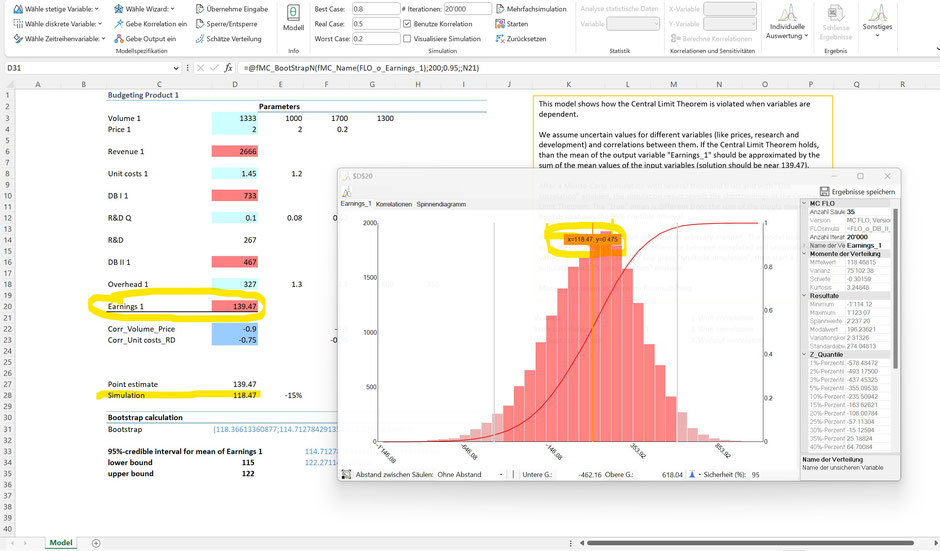
Wie aus der obigen Berechnung (siehe Beispieldatei "The_flaw_of_the_Central_Limit_Theorem.xls") ersichtlich, resultiert ein  Erwartungswert (umgangssprachlich entspricht der Erwartungswert auch dem Mittelwert) von 118.47 für die resultierende Verteilung "Earnings_1" (siehe auch Zelle D28). Dieser Erwartungswert schwankt jedoch von Simulation zu Simulation und weicht von einem statisch hergeleiteten Erwartungswert (siehe Zelle D20) im Regelfall ab. Würden wir die Simulation erneut durchführen, würden wir einen 118.47 abweichenden Erwartungswert bekommen. Die Abweichung hängt dabei u.a. von der Anzahl Iterationen ab, mit der die Simulation durchgeführt wurde. Die Kennzahlen oder auch Lageparameter einer Verteilung sind somit ebenfalls mit Unsicherheit behaftet. 

Mit der Methode Bootstrap erstellen Sie mehrere Stichproben aus der resultierenden Verteilung, womit ein Vertrauensintervall für die Lageparameter erstellt werden kann.  

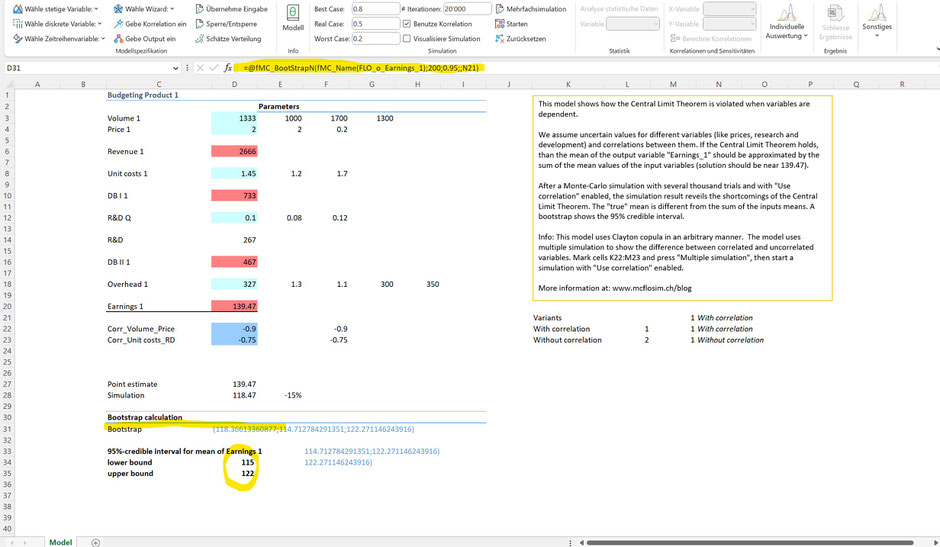
Im obigen Bild wurde ein Bootstrap für die resultierende Verteilung der Variable "Earnings_1" auf Basis des Erwartungswertes mit 200 Stichproben durchgeführt. Als Resultat des 95% Konfidenzintervalls (oder auch Vertrauensintervall) resultiert eine untere Grenze von 115 und eine obere Grenze von 122 (siehe Zellen D34 und D35).   

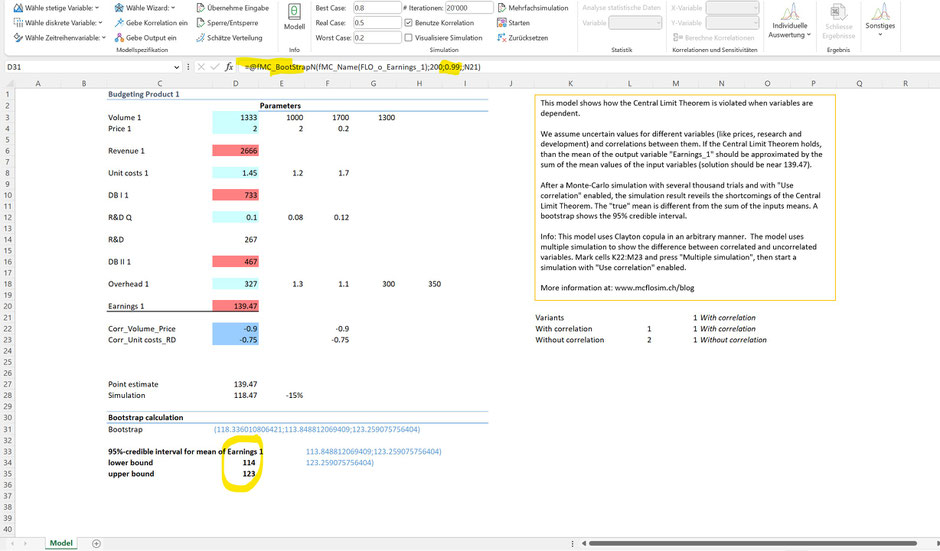
Würden wir die Simulation immer und immer wieder neu starten, würden in 95% der Fälle alle errechneten Vertrauensintervalle den "wahren" Erwartungswert der Variable "Earnings_1" enthalten. Möchten wir uns in weniger als 5% "irren", ist das Vertrauensintervall grösser einzustellen. Anbei das Resultat zum Mittelwert mit einer Sicherheit von 99%:  

Nun sind Werte zwischen 114 und 123 in 99% der Fälle anzunehmen. Wie wir sehen, hat sich auch die erste Zahl in der Klammer geändert (Zelle E31). Diese Zahl stellt den neuen Erwartungswert aller gezogenen Stichproben dar. Da wir 200 Stichproben mit einer Grösse von 20'000 Elementen (Anzahl der durchgeführten Iterationen bei der unterstellten Simulationsberechnung) erheben, können natürlich auch hier leichte Abweichungen resultieren. Sie können natürlich die Anzahl der Stichproben erhöhen, um insgesamt ein stabileres Resultat zu bekommen. Als Faustregel geben wir an, dass die Anzahl Stichproben ca. 10-30% der Anzahl Iterationen entsprechen sollte. 

So das war es. 

Mit Bootstrap können Sie die berechneten Lageparameter einer resultierenden Verteilungen einem Vertrauensbereich zuordnen. Denn auch mit einer Simulation gilt, dass die berechneten Werte nicht als absolut zu interpretieren sind.  

P.S.: Das Verfahren des bootstrap können Sie sogar flexibel zur Bestimmung der "Likelihood" bei der Bayesschen Analyse verwenden, siehe auch folgenden Blogbeitrag.