- Deutsch
- Español
- English
- Blog
- Get it now!
- Shop
- Wiki
- DEU - Stetige Verteilungen
- Gleichverteilung
- Dreiecksverteilung
- Normalverteilung
- LogNormalverteilung
- Betaverteilung
- Gumbelverteilung
- Gammaverteilung
- Exponentialverteilung
- Gekürzte Normalverteilung
- Weibullverteilung
- Pareto-Verteilung
- Cauchy-Verteilung
- ArcSin-Verteilung
- F-Verteilung
- Student-t-Verteilung
- chi2-Verteilung
- PERT-Verteilung
- Fréchet-Verteilung
- Logistische Verteilung
- DEU - Diskrete Verteilungen
- DEU - Zeitreihen
- DEU - Weitere Funktionen
- Referenz
- Umgang mit Variablen
- Interpretation
- Benutzerdefinierte Verteilung
- Begrenzte Verteilungen
- Korrelationen
- Memory Calculation
- Output
- Multiple Simulation / Box-Whisker
- Bayes-Faktor
- Forecast-Tool
- Batch-Funktion
- Datenanpassung
- Benford Analyse
- Dos and don'ts
- Bootstrap
- Decision Information Package
- Spider Diagramm
- Naive Bayes Klassifikation
- Risikomatrix
- DEU - Stetige Verteilungen
Was sind Korrelationen und wie sind diese zu interpretieren?
Korrelationen bilden ein zentrales Element der Simulation dar. Mit Korrelationen wird zum Ausdruck gebracht, dass die Beziehung zwischen Grössen (etwa Preis und Menge) nicht linear und vor allem nicht unabhängig ist.
Oder anders: Korrelationen stellen quantifizierte Abhängigkeiten über Wahrscheinlichkeiten dar.
In der obigen Graphik ist eine Korrelation von -0.85 zwischen Preis und Menge abgetragen (der unter von -0.85 erscheinende Wert von -0.84 gibt den tatsächlichen Rang-Korrelationskoeffizienten wieder). Hierbei ist auf der x-Achse die Variable 1 (Preis) und auf der y-Achse die Variable 2 (Menge) ersichtlich. So sehen wir, dass bei tiefen Preisen (bei ca. 254) das Maximum an verkaufter Menge (ca. 1'100) erreichbar ist, die Wahrscheinlichkeit hierfür ist aber abnehmend. Mit zunehmenden Preisen wird somit eine tiefere Nachfrage antizipiert. Bei einem Preis von 322 ist die Wahrscheinlichkeit, eine Menge von 1'100 abzusetzen, praktisch Null.
Das Phänomen, dass bei höheren Preisen eine tiefere Absatzmenge beobachtet werden kann, ist in der Praxis gegenwärtig.
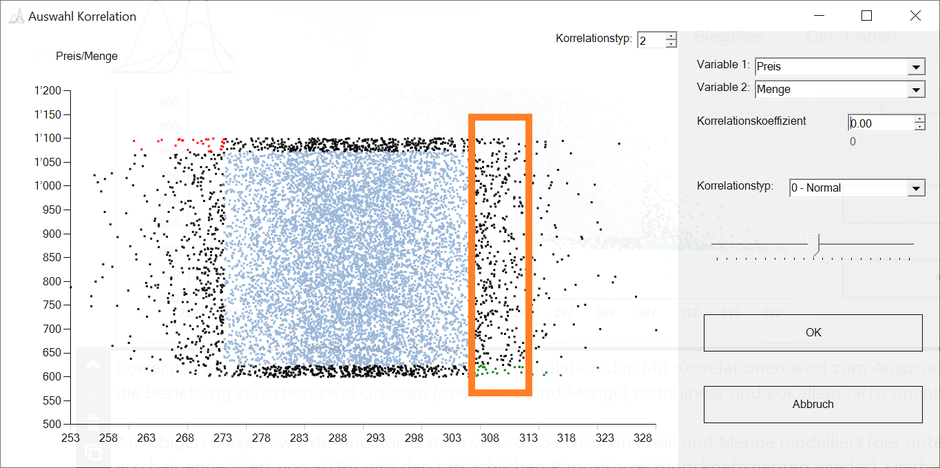
Ein Modell, welches hingegen Unabhängigkeit der Variablen voraussetzt und damit einen Korrelationskoeffizienten von Null annimmt, widerspricht in den meisten Fällen der Beobachtung. Die nachfolgende Graphik des gleichen Sachverhalts, diesmal aber mit einem Korrelationskoeffizienten von Null, zeigt dies eindrücklich:
So ist ersichtlich, dass bei relativ hohen Preisen (etwa bei 310, siehe Rechteck) sowohl eine hohe als auch eine tiefe Absatzmenge gleich wahrscheinlich ist. Auch bei sehr hohen Preisen, etwa bei 320, sind hohe Absatzmengen weiterhin möglich. Wer bei der Modellbildung zwischen Preis und Menge Unabhängigkeit voraussetzt, nimmt somit in Kauf, dass bei hohen Preisen eine hohe Absatzmenge realistisch ist oder umgekehrt bei tiefen Preisen auch eine tiefe Absatzmenge mit gleicher Wahrscheinlichkeit beobachtbar sein sollte.
Auch bei nicht sozio-ökonomischen Fragestellungen sind Korrelationen beobachtbar. So ist bei gutem Wetter der Ernteerfolg höher als bei tiefem Wetter. Aber nicht immer. Auch bei gutem Wetter kann es vorkommen, dass die Ernte schlecht ausfällt, etwa aufgrund einer Heuschreckenplage. Aber es ist nicht genau vorhersagbar. Daher streuen die Werte um eine imaginäre Linie.
Neben der Berücksichtigung von Korrelationen ist auch die Art der Korrelation von Relevanz. Bei der einleitend dargestellten Korrelation ist die Art der Korrelation anhand einer Normal oder Gauss-Copula beschrieben. Es gibt viele Arten (oder auch Copulas), wie Korrelationen abgebildet werden können. Anbei der gleiche Sachverhalt, mit einer Clayton Copula erzeugt:
Hier ist bei tiefen Preisen eine sehr hohe Wahrscheinlichkeit gegeben, eine hohe Absatzmenge zu erzielen. Aber ab einem bestimmten Preispunkt sind sowohl hohe als auch tiefe Absatzmengen möglich.
MC FLO wählt für alle Korrelationsarten den (Pearson) Korrelationskoeffizienten als Formgebung, auch wenn Copulas über verschiedene Formgebungsverfahren verfügen; die Auswahl auf den Korrelationskoeffizienten ist einfacher. Beachten Sie zudem, dass der effektive Korrelationskoeffizient (oben bei -0.74) vom eingesetzten Korrelationskoeffizienten (hier -0.85) abweichen kann; dies ist dann der Fall, wenn nur wenige Daten (Iterationen) herangezogen und/oder von der Gauss-Copula abweichende Korrelationsarten genommen werden.
Die Wahl der Copula als auch die Ausprägung des Korrelationskoeffizienten ist zukunftsbezogen. Vergangene Daten können nur eine Hilfestellung bieten. Zur Zukunftsbezogenheit (insbesondere bei der Unternehmensplanung) wird auf folgenden Blogbeitrag verwiesen.
Info: Für Wertepaare, bei welche beide Punkte (x,y) über (positive) oder unter (negative Korrelation) dem 90% Sicherheitsniveau zu liegen kommen, werden die Punkte in grüner Farbe dargestellt; für Wertepaare, bei welche beide Punkte (x,y) welche unter (negative) oder über (positive Korrelation) dem 90% Sicherheitsniveau zu liegen werden, werden in roter Farbe dargestellt. Für Wertepaare, für welche ein Punkt (x oder y) über dem Sicherheitsniveau von 90% liegen, werden die Punkte in schwarzer Farbe dargestellt, andernfalls werden die Wertepaare in blauer Farbe dargestellt.
Weitere Informationen zu den Korrelationen und insbesondere den Copulas können hier entnommen werden.